Ctrl+K

El paquete Numpy

El paquete Numpy#

Introducción
Tipos
Creación de arrays
Atributos de los arrays
Manipulando arrays
Álgebra lineal
Combinando matrices
Copia
Iterando con bucles
Funciones universales
Ejemplo de aplicación

Introducción#

NumPy, Numeric Python, es un paquete que dispone de múltiples herramientas para manejar matrices de una forma muy eficiente.

En Python ya hemos trabajado con vectores (matriz unidimensional) y matrices usando listas. Dos de las características que dotan de flexibilidad a las listas son:

  • poder albergar distintos tipos de datos en una misma lista

  • poder variar su tamaño de forma dinámica

Esta flexibilidad se consigue con una estructura interna en memoria que penaliza severamente la manipulación eficiente de listas de gran tamaño. ¡No hay beneficio sin servidumbre!

Por otro lado, la inmensa mayoría de las aplicaciones de interés que manejan matrices se caracterizan porque los datos que las conforman son del mismo tipo. Esta es una de las características de las matrices de Numpy: todos sus datos son del mismo tipo, lo que permite un almacenamiento interno en memoria eficiente, usando tipos POD.

Un bloque de memoria asociado a un tipo POD (Plain Old Data) se caracteriza por:

  • El número de celdas (bytes) que lo componen es fijo

  • Las celdas son contiguas

  • Hay un único valor representado, no hay información accesoria ni metadatos

En definitiva, para este tipo de datos, tipos simples, lisos, su representación interna binaria se limita a codificar el valor. Por ejemplo, los tipos fundamentales de lenguajes como C/C++ son POD.

Otro hándicap de Python a la hora de manejar grandes volúmenes de datos es su carácter interpretado. El acceso secuencial vía bucles a todos y cada uno de los elementos de una matriz de gran tamaño conlleva una ejecución, por parte del intérprete, inevitablemente lenta. Para contrarrestar este severo inconveniente, el paquete NumPy permite invocar multitud de métodos de forma vectorizada, es decir, pasando como argumento directamente la variable que representa a la matriz, estando la manipulación secuencial a cargo de una implementación eficiente interna en los lenguajes C o Fortran, y de forma transparente al programador.

Con la vectorización Numpy ni mucho menos ha inventado la rueda. Muchos lenguajes, como C++, permiten implementar funciones vectorizadas, es decir, funciones cuyos argumentos son matrices u operadores cuyos operandos son matrices. El quiz está en que, en Numpy, detrás del escenario, entra en acción una implementación eficiente en un lenguaje compilado.

Para usar NumPy debemos importar el módulo numpy, típicamente usando el alias np:

import numpy as np

Por consistencia con la denominación dentro del módulo, la terminología que usaremos para referirnos indistintamente a vectores y matrices es el barbarismo array.

Debe tenerse en cuenta que en este tema expondremos una pequeña parte de las funciones del módulo NumPy, las que se corresponden con las aplicaciones más habituales. Además, para cada función, existen múltiples alternativas de invocación, con diferentes comportamientos en base a los tipos de los argumentos, argumentos opcionales, etc.

Por otro lado, memorizar todas las posibilidades no tiene sentido, ni en ésta ni en ninguna biblioteca o módulo. Lo importante es conocer las características fundamentales del módulo y aprender a consultar teniendo a mano la documentación pertinente: Numpy reference. Esto último es extensible, en general, a cualquier biblioteca de Python u otro lenguaje.

Tipos#

NumPy permite trabajar con una gran variedad de tipos POD, equivalentes a los tipos fundamentales de C/C++.

De forma implícita, Numpy deduce las constantes literales de la siguiente forma:

  • Literales enteras como 53 al tipo POD numpy int32, representación de enteros en complemento a 2 de 32 bits

  • Literales reales como 3.21 al tipo POD numpy float64, representación de reales IEEE-754 de 64 bits

Si en alguna aplicación se desea utilizar un tipo específico basta indicarlo de forma explícita al crear las matrices, como iremos viendo en los siguientes apartados. Por ejemplo, algunos tipos habituales son:

  • float32, representación de reales IEEE-754 de 32 bits

  • uint8, representación de enteros sin signo de 8 bits

  • int64, representación de enteros en complemento a 2 de 64 bits

  • uint32, representación de enteros sin signo de 32 bits

Creación de arrays#

El módulo Numpy introduce en escena un nuevo tipo de objeto, ndarray (n dimensional array), caracterizado por:

  • Almacenamiento eficiente de colecciones de datos del mismo tipo

  • Conjunto de métodos que permiten operar de forma vectorizada sobre sus datos

Las formas más habituales de crear un nuevo array son:

  • A partir de otras colecciones de datos de Python, como listas o tuplas

  • Desde cero mediante funciones específicas

  • Leyendo los datos de un fichero

A partir de listas#

Para ello se dispone de la función array():

np.array([1, 3, 5, 7, 9, 2, 4, 6, 8])

array([1, 3, 5, 7, 9, 2, 4, 6, 8])

np.array([[1, 3, 5], [7, 9, 2], [4, 6, 8]])

array([[1, 3, 5],
       [7, 9, 2],
       [4, 6, 8]])

Si hay mezcla de tipos, se promocionan los tipos al de mayor rango, siempre que sea legal.

np.array([[1, 3, 5], [7., 9., 2.], [4, 6, 8]])

array([[1., 3., 5.],
       [7., 9., 2.],
       [4., 6., 8.]])

np.array(range(1, 10))

array([1, 2, 3, 4, 5, 6, 7, 8, 9])

Podemos imponer el tipo de dato del array en un argumento opcional, mediante la palabra clave dtype:

np.array([x**2 for x in range(20)], dtype=float)

array([  0.,   1.,   4.,   9.,  16.,  25.,  36.,  49.,  64.,  81., 100.,
       121., 144., 169., 196., 225., 256., 289., 324., 361.])

Desde cero a partir de funciones específicas#

Hay múltiples funciones que permiten inicializar arrays con valores predeterminados, evitando su introducción manual. Mostramos algunas de ellas.

zeros(): inicialización con todos los valores a 0

# El tipo de dato que genera zeros() es por defecto float. 
np.zeros(10)

array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

# Para arrays de dimensión 2 o superior, el argumento con las dimensiones del array son tuplas
dimensiones = (2, 3)
np.zeros(dimensiones, dtype=int)  # np.zeros((2, 3), dtype=int)

array([[0, 0, 0],
       [0, 0, 0]])

ones(): inicialización con todos los valores a 1

# El tipo de dato que genera ones() es por defecto `float`
np.ones(10)

array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

np.ones((2, 3), dtype=int)

array([[1, 1, 1],
       [1, 1, 1]])

full(): inicialización con todos los valores a un valor predeterminado

# El tipo de dato coincide con el del dato de inicialización 
np.full(10, 3)

array([3, 3, 3, 3, 3, 3, 3, 3, 3, 3])

arange(): emula la secuencia nativa de Python range()

La diferencia es que ahora podemos usar límites y pasos con valores reales.

# Secuencia lineal que empieza en 0 y acaba antes de 10. El incremento por defecto es 1.
np.arange(10)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# Secuencia lineal que empieza en 0., acaba antes de 100., con pasos de 2.5 en 2.5
np.arange(0., 100., 2.5)

array([ 0. ,  2.5,  5. ,  7.5, 10. , 12.5, 15. , 17.5, 20. , 22.5, 25. ,
       27.5, 30. , 32.5, 35. , 37.5, 40. , 42.5, 45. , 47.5, 50. , 52.5,
       55. , 57.5, 60. , 62.5, 65. , 67.5, 70. , 72.5, 75. , 77.5, 80. ,
       82.5, 85. , 87.5, 90. , 92.5, 95. , 97.5])

linspace(): crea una secuencia de valores equidistantes entre dos valores límite

# Secuencia lineal con 9 valores equidistantes, que empieza en 0 y acaba en 2
np.linspace(0, 2, 9)

array([0.  , 0.25, 0.5 , 0.75, 1.  , 1.25, 1.5 , 1.75, 2.  ])

diag(): crea una matriz diagonal cuadrada

# El tamaño de la matriz coincide con el de la lista o ndarray 
np.diag([3, 5, 7, 9])

array([[3, 0, 0, 0],
       [0, 5, 0, 0],
       [0, 0, 7, 0],
       [0, 0, 0, 9]])

np.diag(np.ones(5))

array([[1., 0., 0., 0., 0.],
       [0., 1., 0., 0., 0.],
       [0., 0., 1., 0., 0.],
       [0., 0., 0., 1., 0.],
       [0., 0., 0., 0., 1.]])

random.random(): inicialización de valores aleatorios distribuidos uniformemente

# Matriz de dimensiones (2,3) con valores aleatorios uniformes en el intervalo semiabierto [0,1)
np.random.random((2, 3))

array([[0.05218103, 0.14480041, 0.9716879 ],
       [0.38485644, 0.18211548, 0.42006346]])

Para obtener una distribución uniforme en el intervalo semiabierto \([a,b)\), con \(b>a\) basta con premultiplicar por \(b-a\) y al resultado sumarle \(a\).

# Matriz de dimensiones (2,3) con valores aleatorios uniformes en el intervalo semiabierto [-2,2)
4*np.random.random((2, 3)) - 2

array([[ 1.29491978,  1.96514488,  1.18200861],
       [-1.49282516, -0.88104159,  1.06784748]])

random.normal(): inicialización de valores aleatorios con una distribución normal

# Vector de dimensión 10 con valores aleatorios con distribución normal de media 0 y desviación estándar 1
np.random.normal(0, 1, 10)

array([-0.47262837, -0.55047765,  2.01764747,  0.46417102, -0.3746389 ,
        1.45309969, -0.18800919, -0.15918058, -0.52739722, -0.02707597])

random.randint(): inicialización de valores aleatorios enteros pertenecientes a un rango de valores

# Matriz 5x5 de enteros aleatorios en el intervalo abierto [-9, 10)
np.random.randint(-9, 10, (5, 5))

array([[-8, -3, -7, -6, -8],
       [ 6,  4,  3, -7, -5],
       [-5,  0, -8, -1, -6],
       [ 6,  7,  1, -5,  9],
       [-3,  1,  9, -9,  3]])

Como ejemplo de la ingente cantidad de funciones de Numpy, echad un ojo al enlace Numpy random reference, que muestra la variedad de herramientas para trabajar con números aleatorios.

Desde un fichero#

Ficheros de texto#

El fichero ejemplo_con_espacios_en_blanco.dat tiene un conjunto de datos separados por espacios en blanco.

1 2   3
4  5 6
7 8   9
   10 11 12

La función loadtxt() es capaz de leerlo de forma inmediata, siendo el tipo de dato por defecto float.

np.loadtxt('data/ejemplo_con_espacios_en_blanco.dat')

array([[ 1.,  2.,  3.],
       [ 4.,  5.,  6.],
       [ 7.,  8.,  9.],
       [10., 11., 12.]])

# Leyendo como tipo int
np.loadtxt('data/ejemplo_con_espacios_en_blanco.dat', dtype=int)

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

Si el fichero tiene sus datos separados por un delimitador homogéneo, como la , en los ficheros .csv, (comma separated values), el uso del parámetro opcional delimiter filtra ese carácter. Es el caso del fichero ejemplo_csv.dat

1,2,3
4,  5, 6
7 ,8 ,  9
   10, 11, 12

La función loadtxt() es capaz de leerlo de forma inmediata, siendo el tipo de dato por defecto float. Nótese en ambos ejemplos la deliberada introducción de espacios en blanco innecesarios.

np.loadtxt('data/ejemplo_csv.dat', dtype=int, delimiter=',')

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

De nuevo, las posibilidades de lectura de un fichero que ofrece Numpy es enorme. Imaginemos un tipo de fichero, ejemplo_lectura_parcial.dat del que sabemos que las dos primeras filas describen el archivo y no estamos interesados en ellas.

Las dos primeras líneas describen el fichero
Además, en el ejemplo, solo queremos leer la segunda y tercera columna
1 3.123 23
2 4.53 12
3 6.71 17
4 9.3 15
5 2.731 9
6 29.14 106

El parámetro opcional skiprows nos permite hacerlo fácilmente.

Además, de entre los datos útiles solo estamos interesados en las columnas 1 y 2. Con el parámetro opcional usecols podemos seleccionar las columnas.

M = np.loadtxt('data/ejemplo_lectura_parcial.dat', skiprows=2, usecols=(1, 2))
print(M)

[[  3.123  23.   ]
 [  4.53   12.   ]
 [  6.71   17.   ]
 [  9.3    15.   ]
 [  2.731   9.   ]
 [ 29.14  106.   ]]

Volvemos a insistir que la manera de proceder para aprender a trabajar con este y otros módulos no es memorizar comandos, sino consultar el manual de referencia correspondiente y sondear todas las posibilidades que una determinada herramienta ofrece. Para el caso de la función loadtxt(), el enlace al manual de referencia es numpy.loadtxt reference.

Como el alumno podrá imaginar, existe una función hermana de loadtxt().

# Salvar en el archivo data/prueba.dat la matriz m generada en la celda anterior en formato csv
# con un formato de solo dos cifras decimales para la primera columna y enteros para la segunda

np.savetxt('data/prueba.dat', M, delimiter=',', fmt=['%.2f', '%d'])
np.loadtxt('data/prueba.dat', delimiter=',')

array([[  3.12,  23.  ],
       [  4.53,  12.  ],
       [  6.71,  17.  ],
       [  9.3 ,  15.  ],
       [  2.73,   9.  ],
       [ 29.14, 106.  ]])

Ficheros binarios#

Numpy maneja su propio formato nativo de ficheros a través de las funciones save() y load(). El almacenamiento es de tipo binario y, por tanto, no son legibles. En ausencia de extensión, se añade la terminación .npy. Es la mejor alternativa de lectura/escritura por su eficiencia y comodidad si nos vamos a mover dentro del universo Numpy.

np.save('data/fichero_numpy', M)
np.load('data/fichero_numpy.npy')

array([[  3.123,  23.   ],
       [  4.53 ,  12.   ],
       [  6.71 ,  17.   ],
       [  9.3  ,  15.   ],
       [  2.731,   9.   ],
       [ 29.14 , 106.   ]])

Atributos de los arrays#

Las dimensiones de un array se pueden obtener con el atributo shape, que devuelve una tupla.

M = np.ones((2, 3), dtype=float)
M.shape

(2, 3)

Para acceder al número de elementos se dispone del atributo size:

M.size

6

El número de dimensiones se almacena en el atributo ndim:

M.ndim

2

Se puede obtener también consultando la longitud de la tupla shape.

len(M.shape)

2

Manipulando arrays#

Indexado#

Para arrays unidimensionales, se hace de forma equivalente a las listas:

v = np.random.randint(-9, 10, 5)
print(v)
v[0]

[-9 -9  8 -7 -1]

-9

Para arrays multidimensionales, accedemos individualmente a los elementos, que son valores escalares, separando los índices por comas:

M = np.random.randint(-9, 10, (5, 3))
print(M)
M[1, 2]

[[-3  6  7]
 [-8 -5 -3]
 [-8  5 -8]
 [-9 -5  5]
 [-5  5 -2]]

-3

Es relevante indicar que el tipo de los escalares indexados corresponde al mismo tipo del que tiene el array. En general, la mezcla de tipos no genera ningún problema, promocionándose en todo caso al de mayor rango.

v = np.array([4, 3, 5, 7], dtype='uint8')
x = v[0]
y = 8  # Tipo nativo Python int
z = x*y
w = int(z)  # Podemos convertir el tipo a uno nativo de Python

print(f'x = {x}, que es de tipo {type(x)}')
print(f'y = {y}, que es de tipo {type(y)}')
print(f'z = {z}, que es de tipo {type(z)}')
print(f'w = {w}, que es de tipo {type(w)}')

x = 4, que es de tipo <class 'numpy.uint8'>
y = 8, que es de tipo <class 'int'>
z = 32, que es de tipo <class 'numpy.int32'>
w = 32, que es de tipo <class 'int'>

Si queremos acceder, por ejemplo, a toda una fila de una matriz de dos dimensiones, indicamos simplemente el índice de la fila:

M[1]

array([-8, -5, -3])

Lo mismo se puede conseguir usando la notación ::

M[2, :]  # fila 2

array([-8,  5, -8])

Esto nos permite de una forma práctica acceder a toda una columna:

M[:, 1]  # columna 1

array([ 6, -5,  5, -5,  5])

Las asignaciones a elementos individuales siguen las pautas normales:

M[1, 2] = 1000

M

array([[  -3,    6,    7],
       [  -8,   -5, 1000],
       [  -8,    5,   -8],
       [  -9,   -5,    5],
       [  -5,    5,   -2]])

También podemos asignar un valor a todos los elementos de una fila o columna:

M[2, :] = 10000
M[:, 1] = -300

M

array([[   -3,  -300,     7],
       [   -8,  -300,  1000],
       [10000,  -300, 10000],
       [   -9,  -300,     5],
       [   -5,  -300,    -2]])

Álgebra lineal#

El paquete NumPy permite invocar multitud de métodos de forma vectorizada, es decir, pasando como argumento directamente la variable que representa a la matriz.

Operaciones de tipo escalar#

Veamos algunos ejemplos:

v = np.arange(0, 10)

2*v

array([ 0,  2,  4,  6,  8, 10, 12, 14, 16, 18])

v + 3

array([ 3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

M = np.ones((3, 5))

2*M

array([[2., 2., 2., 2., 2.],
       [2., 2., 2., 2., 2.],
       [2., 2., 2., 2., 2.]])

M - 1

array([[0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0.]])

Operaciones entre elementos correlativos#

Las operaciones aritméticas operan entre elementos correlativos. Lógicamente, las dimensiones de las matrices involucradas deben ser compatibles.

M = np.array([[1, 2, 3], [4, 5, 6]])
N = np.ones((2, 3))
M + N

array([[2., 3., 4.],
       [5., 6., 7.]])

M*M

array([[ 1,  4,  9],
       [16, 25, 36]])

v = np.arange(0, 3)
v*v

array([0, 1, 4])

Operaciones con matrices#

De nuevo, las dimensiones de las matrices involucradas deben ser compatibles.

Multiplicación#

Usando la función dot:

M = np.array([[1, 2, 3], [4, 5, 6]])
N = np.array([[1, 2], [3, 4], [5, 6]])
M.shape, N.shape

((2, 3), (3, 2))

np.dot(M, N)

array([[22, 28],
       [49, 64]])

v = np.arange(0, 3)
M.shape, v.shape

((2, 3), (3,))

np.dot(M, v)

array([ 8, 17])

El producto escalar#

np.dot(v, v)  # producto escalar

5

Hacemos aquí un breve inciso para recordar las grandes ventajas que aportan las funciones, encapsulando el código y proporcionando abstracción.

v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])

prod_esc = np.dot(v1, v2)  # producto escalar
print(prod_esc)

# Fijaos que dot() es una forma compacta de la siguiente
prod_esc = np.sum(v1*v2)  #np.sum es el sumatorio de los elementos de un vector
print(prod_esc)

# Esta última a su vez es una forma compacta de la siguiente
prod_esc = 0
for x, y in zip(v1, v2):
    prod_esc += x*y
print(prod_esc)

# Y esta última a su vez es una forma menos verbosa de la siguiente
prod_esc = 0
for i in range(len(v1)):
    prod_esc += v1[i]*v2[i]
print(prod_esc)

32
32
32
32

El producto vectorial#

La función cross() está definida pensando en el espacio tridimensional de los reales. Por tanto, se espera vectores de dimensión 2 y/o 3. Si la dimensión de alguno de los vectores es 2, se interpreta que la coordenada \(z\) es nula.

u_x = np.array([1, 0, 0])  # Vector unitario eje X
u_y = np.array([0, 1, 0])  # Vector unitario eje Y
u_z = np.cross(u_x, u_y)
print(u_z)

[0 0 1]

Transformaciones#

Transpuesta#

Mediante .T o la función transpose podemos obtener la transpuesta.

M = np.array([[1, 2, 3], [4, 5, 6]])
M.T

array([[1, 4],
       [2, 5],
       [3, 6]])

np.transpose(M)

array([[1, 4],
       [2, 5],
       [3, 6]])

Inversa#

Debemos invocar al módulo de álgebra lineal linalg.

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 10]])
N = np.linalg.inv(M) 
print(N)

[[-0.66666667 -1.33333333  1.        ]
 [-0.66666667  3.66666667 -2.        ]
 [ 1.         -2.          1.        ]]

np.dot(M, N)

array([[ 1.00000000e+00, -4.44089210e-16, -1.11022302e-16],
       [ 4.44089210e-16,  1.00000000e+00, -2.22044605e-16],
       [ 4.44089210e-16,  8.88178420e-16,  1.00000000e+00]])

Determinante#

np.linalg.det(M)

-3.000000000000001

Propiedades de la matriz#

Media#

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
np.mean(M)  # Media de todos los valores de la matriz

5.0

np.mean(M[:, 2])  # Media de la columna 2

6.0

np.mean(M[0, :])  # Media de la fila 0

2.0

Desviación estándar y varianza#

np.std(M), np.var(M)

(2.581988897471611, 6.666666666666667)

np.std(M[:, 2]), np.var(M[0, :])

(2.449489742783178, 0.6666666666666666)

Norma#

Podemos utilizar la expresión del producto escalar: \(||u|| = \sqrt{u \bullet u}\)

u = np.array([1, 1, 1])
norma = np.sqrt(np.dot(u,u))
print(norma)

1.7320508075688772

Sin embargo, dentro del módulo linalg tenemos la función norm() que permite su cálculo de forma más cómoda.

norma = np.linalg.norm(u)
print(norma)

1.7320508075688772

Mínimo y máximo#

M.min(), M.max()

(1, 9)

M[:, 2].min(), M[:, 2].max()

(3, 9)

Suma y producto de los elementos, suma y producto acumulativos y traza#

np.sum(M)

45

np.prod(M)

362880

# Suma acumulativa. Recorre por filas.
np.cumsum(M)

array([ 1,  3,  6, 10, 15, 21, 28, 36, 45])

# Producto acumulativo. Recorre por filas.
np.cumprod(M)

array([     1,      2,      6,     24,    120,    720,   5040,  40320,
       362880])

# Podría usarse npdiag(M).sum()
np.trace(M)

15

Combinando matrices#

Hay muchas opciones. Vamos a comentar unas pocas.

Concatenar#

v1 = np.array([1, 2, 3])
v2 = np.array([4, 5, 6])
v3 = np.array([7, 8, 9])

M = np.concatenate((v1, v2, v3))
print(M)

[1 2 3 4 5 6 7 8 9]

Apilar, horizontal y verticalmente#

M = np.vstack((v1, v2, v3))
print(M)

[[1 2 3]
 [4 5 6]
 [7 8 9]]

M = np.hstack((v1, v2, v3))  # El mismo resultado para este ejemplo que concatenate
print(M)

[1 2 3 4 5 6 7 8 9]

Copia#

Para obtener una copia independiente de una matriz se usa el método copy()

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
N = np.copy(M)

N [0, 0] = -1000
N

array([[-1000,     2,     3],
       [    4,     5,     6],
       [    7,     8,     9]])

M

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

Iterando con bucles#

Se opera de forma similar a como se hace con listas:

v = np.arange(10)

for x in v:
    print(x)

0
1
2
3
4
5
6
7
8
9

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

for fila in M:  # fila es una fila de M
    for x in fila:
        print(x, end=' ')
    print()

1 2 3 
4 5 6 
7 8 9

Para iterar y modificar, nos podemos ayudar de enumerate().

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Elevamos al cuadrado los elementos de la matriz M
for i, fila in enumerate(M):  # i es el índice de la fila; fila es una fila de M
    for j, x in enumerate(fila):
        M[i, j] *= x
        
print(M)

[[ 1  4  9]
 [16 25 36]
 [49 64 81]]

Hubiera sido más simple hacer lo siguiente:

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
M = M*M
print(M)

[[ 1  4  9]
 [16 25 36]
 [49 64 81]]

O incluso mejor:

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
M = M**2
print(M)

[[ 1  4  9]
 [16 25 36]
 [49 64 81]]

Estos dos ejemplos anteriores muestran que en muchas ocasiones las operaciones que iteran sobre los elementos de una matriz ya están implementadas en Numpy. ¡No reinventemos la rueda!

Funciones universales#

Una función universal es una función que realiza operaciones elemento a elemento de la matriz. Gran parte de las funciones de la biblioteca matemática están vectorizadas en el módulo Numpy.

M = np.array([np.pi, np.pi/2, np.pi/3, np.pi/4, 0])
np.cos(M)

array([-1.00000000e+00,  6.12323400e-17,  5.00000000e-01,  7.07106781e-01,
        1.00000000e+00])

M = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
np.sqrt(M)

array([[1.        , 1.41421356, 1.73205081],
       [2.        , 2.23606798, 2.44948974],
       [2.64575131, 2.82842712, 3.        ]])

Podéis consultar todas las opciones disponibles en numpy.ufuncs reference

Ejemplo de aplicación#

Planos y rectas en el espacio euclídeo 3D#

Aviso

Este apartado utiliza raise del tema Manejo de excepciones. Si no lo has estudiado, una opción es sustituir raise por un mensaje de error y devolver None.

En este ejemplo se repasan algunos conceptos acerca de rectas y planos en el espacio euclídeo 3D.

Normalización de un vector#

Consiste en dividir los elementos de un vector \(\mathbf{v}\) por su norma para hacerlo unitario.

\[\hat{\mathbf{v}}=\frac{\mathbf{v}}{||\mathbf{v}||}\]

El parámetro v puede ser una lista, tupla o numpy array (lo recomendado). Se levanta una excepción si la norma del vector es inferior a una tolerancia predeterminada.

def normaliza(v, tol=1e-6):
    '''
    Devuelve, sin alterarlo, el vector normalizado de v.
    
    Parameters
    ----------
    v : list, tuple, numpy.ndarray: numérico
        Vector unidimensional
    tol : float
        Tolerancia que debe cumplir la norma del vector v
    Returns
    -------
    v_norm : numpy.ndarray of floats
        Vector normalizado unitario
    Raises
    ------
    ValueError
        Si la norma del vector inicial es inferior a tol
    Example
    -------
        >>> v = (1, 1, 1)
        >>> normaliza(v)
    '''

    norma = np.linalg.norm(v)
    if norma < tol:
        raise ValueError('La norma del vector es inferior a la tolerancia {}.'.format(tol))
    v_norm = v/norma  # Al usar np.linalg.norm() v_norm es un numpy.ndarray
    return v_norm


v = (1, 1, 1)
normaliza(v)

array([0.57735027, 0.57735027, 0.57735027])

Distancia entre dos puntos 3D#

Dados \(\mathbf{p}_1 = (x_1,y_1,z_1)\) y \(\mathbf{p}_2 = (x_2,y_2,z_2)\), la distancia entre ellos viene dada por:

\[d_{p_1p_2}= ||\mathbf{p}_1-\mathbf{p}_2||\]

Esta función solo admite como parámetros numpy arrays, ya que utiliza con éstos el operador -. Nótese que la función puede utilizarse para vectores de cualquier dimensión.

El valor devuelto es un tipo de dato numpy float.

def distancia_entre_puntos(p1, p2):  # Versión solo válida para numpy arrays
    '''
    Parameters
    ----------
    p1, p2 : numpy.ndarray
        Vectores unidimensionales
    Returns
    -------
    dist : numpy float
        Distancia entre los puntos p1 y p2
    Example:
    --------
    >>> p1 = np.array((1, 1, 1), dtype=float)
    >>> p2 = np.array((2, 3, 4), dtype=float)
    >>> distancia_entre_puntos(p1, p2)
    '''
    dist = np.linalg.norm(p1-p2)  # p1-p2 no está definido para tuplas o listas
    return dist

# Ejemplo distancia_entre_puntos()
p1 = np.array((1, 1, 1))
p2 = np.array((2, 3, 4))
distancia_entre_puntos(p1, p2)

3.7416573867739413

El ángulo que forman dos vectores#

Sabemos del álgebra que \(\mathbf{u} \bullet \mathbf{v} = ||\mathbf{u}||||\mathbf{v}||cos(\theta)\). Por tanto, podemos obtener:

\[\theta = arccos(\frac{\mathbf{u} \bullet \mathbf{v}}{||\mathbf{u}||||\mathbf{v}||})\]
def angulo(v1, v2):
    '''
    Parameters
    ----------
    v1, v2 : tuple, list, numpy.ndarray: numérico
        Vectores unidimensionales
    Returns
    -------
    angulo : float
        Ángulo en radianes que forman los vectores
    Example
    -------
    >>> u_x = [1, 0, 0]  # Vector unitario eje X
    >>> u_y = [0, 1, 0]  # Vector unitario eje Y
    >>> angulo(u_x, u_y)*180/np.pi  # Ángulo en grados
    '''

    prod_esc = np.dot(v1, v2)
    norma_v1 = np.linalg.norm(v1)
    norma_v2 = np.linalg.norm(v2)

    angulo = np.arccos(np.clip(prod_esc/(norma_v1*norma_v2), -1, 1))
    return angulo


u_x = [1, 0, 0]  # Vector unitario eje X
u_y = [0, 1, 0]  # Vector unitario eje Y


ang = angulo(u_x, u_y)
print(ang*180/np.pi)

90.0

La función np.clic(expresion, min, max) es una función que limita el valor de expresion a los límites [min, max]. Aquí se usa porque numéricamente la expresion prod_esc/(norma_v1*norma_v2) puede dar valores del tipo 1.0000000000002 que hacen que el arccos() esté indefinido. Recordad la incapacidad para la representación exacta de la norma IEEE-754.

Formas de parametrizar un plano#

Con un punto y un vector perpendicular al plano

Sea \(\mathbf{p}_0 = (x_0,y_0,z_0)\) un punto del espacio euclídeo 3D y \(\mathbf{n} = (A, B, C)\) un vector no nulo.

Un plano caracterizado por la tupla \((\mathbf{p}_0, \mathbf{n})\) consiste en todos los puntos \(\mathbf{p} = (x,y,z)\) tales que el vector \(\mathbf{v} = \mathbf{p}-\mathbf{p}_0\) es perpendicular a \(\mathbf{n}\).

Esta propiedad es fácil expresarla matemáticamente:

\[(\mathbf{p}-\mathbf{p}_0) \bullet \mathbf{n} = 0 \tag{1}\]

donde \(\bullet\) representa el producto escalar.

Forma algebraica o implícita

Expandiendo (1) es fácil llegar a la expresión algebraica:

\[(\mathbf{p}-\mathbf{p}_0) \bullet \mathbf{n} = \mathbf{p} \bullet \mathbf{n} - \mathbf{p}_0 \bullet \mathbf{n} = Ax+By+Cz+D=0 \tag{2}\]

donde el parámetro \(D\) viene dado por:

\[D=-\mathbf{p}_0 \bullet \mathbf{n} \tag{3}\]

Esta parametrización puede caracterizarse con la tupla \((\mathbf{n}, D)\)

Plano a partir de tres puntos#

Sean \(\mathbf{p}_1 = (x_1,y_1,z_1)\), \(\mathbf{p}_2 = (x_2,y_2,z_2)\) y \(\mathbf{p}_3 = (x_3,y_3,z_3)\) tres puntos diferentes del espacio euclídeo 3D.

Entre las diferentes alternativas, el plano asociado a estos tres puntos puede obtenerse fácilmente con los pasos siguientes:

  1. Se obtiene el vector perpendicular \(\mathbf{n}= (A, B, C)\) según:

    \[\mathbf{n} = (\mathbf{p}_1 - \mathbf{p}_2) \times (\mathbf{p}_1 - \mathbf{p}_3)\]

    donde \(\times\) es el producto vectorial. La idea es que los dos vectores formados a partir de los tres puntos pertenecen al plano y, por tanto, su producto vectorial es la perpendicular \(\mathbf{n}\).

  2. Se escoge cualquiera de los 3 puntos, por ejemplo \(\mathbf{p}_1\) para obtener la tupla \((\mathbf{p}_1, \mathbf{n})\)

Si se desea la forma algebraica dada por (2), basta obtener \(D=-\mathbf{p}_1 \bullet \mathbf{n}\) y el plano vendría determinado por la tupla \((\mathbf{n},D)\)

La función plano_tres_puntos() devuelve la parametrización dada por la tupla \((\mathbf{n},D)\). Además, garantiza que el vector \(\mathbf{n}\) es unitario.

def plano_tres_puntos(p1, p2, p3, tol=1e-3):
    '''
    Parameters
    ----------
    p1, p2, p3 : numpy.ndarray of floats
        Vectores unidimensionales representando 3 puntos 3D
    tol : float
        Tolerancia que deben cumplir las distancias entre los puntos
    Returns
    -------
    n, D : tuple : (numpy.ndarray of float, numpy float)
        n es el vector unitario perpendicular al plano
        D es el término independiente de la ecuación algebraica Ax+By+Cz+D=0
    Raises
    ------
    ValueError
        Si la distancia entre alguno de los 3 puntos es inferior a tol
    Example
    -------
    >>> p1 = np.array((1, 0, 0))
    >>> p2 = np.array((0, 1, 0))
    >>> p3 = np.array((0, 0, 1))
    >>> n, D = plano_tres_puntos(p1, p2, p3)
    '''
    dist12 = distancia_entre_puntos(p1, p2)
    dist13 = distancia_entre_puntos(p1, p3)
    dist23 = distancia_entre_puntos(p2, p3)

    if dist12 < tol or dist13 < tol or dist23 < tol:
        raise ValueError('Distancia entre puntos menor que la tolerancia {}.'.format(tol))

    # Producto vectorial para A B C
    # |  i       j       k    |
    # |v_12[0] v_12[1] v_12[2]|
    # |v_13[0] v_13[1] v_13[2]|

    v12 = p1 - p2
    v13 = p1 - p3

    n = normaliza(np.cross(v12, v13))

    D = -np.dot(n, p1)

    return n, D

p1 = np.array((1, 0, 0))  
p2 = np.array((0, 1, 0))
p3 = np.array((0, 0, 1))
n, D = plano_tres_puntos(p1, p2, p3)
print(n)
print(D)

[0.57735027 0.57735027 0.57735027]
-0.5773502691896258

Formas de parametrizar una recta#

Con dos puntos

Sean \(\mathbf{p}_1 = (x_1,y_1,z_1)\), \(\mathbf{p}_2 = (x_2,y_2,z_2)\) dos puntos diferentes del espacio euclídeo 3D.

Los puntos \(\mathbf{p} = (x,y,z)\) pertenecientes a la recta definida por \(\mathbf{p}_1\) y \(\mathbf{p}_2\) satisfacen la siguiente ecuación vectorial:

\[\mathbf{p} = \mathbf{p}_1 + \lambda (\mathbf{p}_2 - \mathbf{p}_1) \quad \lambda \in \mathbb{R} \tag{4}\]

De esta forma, esta parametrización vendría dada por una tupla \((\mathbf{p}_1, \mathbf{v})\), donde \(\mathbf{v}\) es el vector director, \(\mathbf{v}=\mathbf{p}_2 - \mathbf{p}_1\).

def recta_dos_puntos(p1, p2, tol=1e-3):
    '''
    Parameters
    ----------
    p1, p2 : numpy.ndarray of floats
        Vectores unidimensionales representando 2 puntos 3D
    tol : float
        Tolerancia que debe cumplir la distancia entre los puntos
    Returns
    -------
    p, v : tuple: (numpy.ndarray of float, numpy.ndarray of float)
        p es una copia de p1, punto pasado como primer parámetro

        v es el vector director unitario de la recta
    Raises
    ------
    ValueError
        Si la distancia entre los 2 puntos es inferior a tol
    Example
    -------
    >>> p1 = np.array((2, 2, 2))
    >>> p2 = np.array((3, 3, 3))
    >>> p, v = recta_dos_puntos(p1, p2)
    '''
    if distancia_entre_puntos(p1, p2) < tol:
        raise ValueError('Distancia entre puntos menor que la tolerancia {}.'.format(tol))
    v = normaliza(p1-p2)
    return np.copy(p1), v

# Ejemplo recta_dos_puntos()
p1 = np.array((2, 2, 2))  
p2 = np.array((3, 3, 3))
p, v = recta_dos_puntos(p1, p2)
print(p)
print(v)

[2 2 2]
[-0.57735027 -0.57735027 -0.57735027]

Nótese el uso de np.copy(p1) para que sea un vector ligado a un objeto diferente que p1. Este tipo de detalles suelen ser uno de los mayores quebraderos de cabeza en Python.

Mediante la intersección de dos planos

Dados los planos definidos por las tuplas \((\mathbf{n}_1, D_1)\) y \((\mathbf{n}_2, D_2)\), la recta vendría definida por la pareja de ecuaciones lineales:

\(\begin{align} A_1x+B_1y+C_1z+D_1=0 \\ A_2x+B_2y+C_2z+D_2=0 \end{align} \tag{5}\)

Obviamente, si los vectores \(\mathbf{n}_1\) y \(\mathbf{n}_2\) son paralelos, la expresión (5) no está correctamente definida.

Intersección de una recta y un plano#

Supongamos que nos dan para el plano la tupla \((\mathbf{n}, D)\) y para la recta la ecuación vectorial, dada por la tupla \((\mathbf{p}_0, \mathbf{v})\). Es decir, tenemos las ecuaciones:

\(\begin{align} \quad & \mathbf{n} \bullet \mathbf{p} + D = 0 \\ \quad & \mathbf{p} = \mathbf{p}_0 + \lambda \mathbf{v} \end{align}\)

Sustituyendo \(\mathbf{p}\) arriba obtenemos:

\[\mathbf{n} \bullet (\mathbf{p}_0 + \lambda \mathbf{v}) + D = 0\]

Nos interesa encontrar el valor de \(\lambda\) para el que se produce el corte:

\[\lambda = -\frac{\mathbf{n} \bullet \mathbf{p}_0 + D}{\mathbf{n} \bullet \mathbf{v}} \tag{6}\]

Sustituyendo (6) en (4) se obtiene el punto de intersección \(\mathbf{p}\) de forma inmediata:

\[\mathbf{p} = \mathbf{p}_0 -\frac{\mathbf{n} \bullet \mathbf{p}_0 + D}{\mathbf{n} \bullet \mathbf{v}} \mathbf{v}\]
def interseccion_recta_plano(recta, plano, tol=0.1):
    '''
    Parameters
    ----------
    recta : tuple : (numpy.ndarray of floats, numpy.ndarray of floats)
        Recta definida por la tupla punto inicial y vector director
        p=p_0+l*v
    plano : tuple : (numpy.ndarray of floats, float)
        Plano definido por la tupla vector normal (A, B, C) y término independiente D
        Ax+By+Cz+D=0
    tol : float
        Tolerancia que deben cumplir el ángulo entre recta y plano
    Returns
    -------
    p : numpy.ndarray of floats
        El punto de intersección
    Raises
    ------
    ValueError
        Si el ángulo entre ambas figuras es inferior a tol en radianes
    Example
    -------
    >>> p1 = np.array((1, 0, 0))
    >>> p2 = np.array((0, 1, 0))
    >>> p3 = np.array((0, 0, 1))
    >>> p4 = np.array((2, 2, 2))
    >>> p5 = np.array((3, 3, 3))
    >>> plano = plano_tres_puntos(p1, p2, p3)
    >>> recta = recta_dos_puntos(p4, p5)
    >>> p = interseccion_recta_plano(recta, plano)
    '''
    ang = angulo(recta[1], plano[0])

    if np.abs(ang-np.pi/2) < tol:
        raise ValueError('La recta y el plano son casi paralelos según tolerancia {}.'.format(tol))

    lamb = -(np.dot(recta[0], plano[0])+plano[1])/np.dot(recta[1], plano[0])

    return recta[0] + lamb*recta[1]

# Ejemplo interseccion_recta_plano()
p1 = np.array((1, 0, 0))  
p2 = np.array((0, 1, 0))
p3 = np.array((0, 0, 1))
p4 = np.array((2, 2, 2))
p5 = np.array((3, 3, 3))
plano = plano_tres_puntos(p1, p2, p3)
recta = recta_dos_puntos(p4, p5)
p = interseccion_recta_plano(recta, plano)
print(p)

[0.33333333 0.33333333 0.33333333]

Distancia de un punto a un plano#

Supongamos que nos dan para el plano la tupla \((\mathbf{n}, D)\) y un punto \(\mathbf{p}_0 = (x_0,y_0,z_0)\).

La distancia viene determinada por la longitud del segmento de recta perpendicular al plano, que tiene por extremos el punto \(\mathbf{p}_0\) y su intersección \(\mathbf{p}_i\) con el plano \((\mathbf{n}, D)\).

Veamos cuál es ese punto de intersección:

\(\begin{align} \quad & \mathbf{n} \bullet \mathbf{p}_i + D = 0 \\ \quad & \mathbf{p}_i = \mathbf{p}_0 + \lambda \mathbf{n} \end{align}\)

donde ahora el vector director de la recta es \(\mathbf{n}\).

Sustituyendo en (6):

\[\lambda = -\frac{\mathbf{n} \bullet \mathbf{p}_0 + D}{\mathbf{n} \bullet \mathbf{n}} \tag{7}\]

Por otro lado, la distancia entre \(\mathbf{p}_0\) y cualquier punto \(\mathbf{p}\) de la recta viene dada por la expresión:

\[d=||\mathbf{p}_0 - (\mathbf{p}_0+ \lambda \mathbf{n})||= ||\lambda\mathbf{n}|| = |\lambda|\,||\mathbf{n}||\tag{8}\]

Sustituyendo el valor de \(\lambda\) hallado en (7) en la expresión (8):

\[d=|-\frac{\mathbf{n} \bullet \mathbf{p}_0 + D}{\mathbf{n} \bullet \mathbf{n}}|\,||\mathbf{n}|| = \frac{|\mathbf{n} \bullet \mathbf{p}_0 + D|}{||\mathbf{n}||} \tag{9}\]

donde utilizamos el hecho de que \(\mathbf{n} \bullet \mathbf{n} = \pm ||\mathbf{n}||^2\).

La expresión (9) es habitual verla en la bibliografía como:

\[d=\frac{|\mathbf{n} \bullet \mathbf{p}_0 + D|}{||\mathbf{n}||}=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} \tag{10}\]

Si trabajamos con un plano cuya vector normal \(\mathbf{n}\) está normalizado, se produce un ahorro de cálculos al quedar la expresión (10) como:

\[d=|Ax_0+By_0+Cz_0+D| \quad con \,||\mathbf{n}||=1 \tag{11}\]
def distancia_punto_plano(plano, punto):
    '''
    Parameters
    ----------
    plano : tuple: (numpy.ndarray of floats, float)
        Plano definido por la tupla vector normal (A,B,C) y término independiente D
        Ax+By+Cz+D=0
    punto : numpy.ndarray of floats
        Vector unidimensional representando 1 punto 3D
    Returns
    -------
    dist : float
        La distancia del punto al plano
    Example
    -------
    >>> p1 = np.array((1, 0, 0))
    >>> p2 = np.array((0, 1, 0))
    >>> p3 = np.array((0, 0, 1))
    >>> p4 = np.array((1, 1, 1))
    >>> plano = plano_tres_puntos(p1, p2, p3)
    >>> dist = distancia_punto_plano(plano, p4)
    '''

    n, D = plano
    n = normaliza(n)
    return np.abs(np.dot(n, punto) + D)

# Ejemplo distancia_punto_plano()
p1 = np.array((1, 0, 0))  
p2 = np.array((0, 1, 0))
p3 = np.array((0, 0, 1))
p4 = np.array((1, 1, 1))
plano = plano_tres_puntos(p1, p2, p3)
print(plano)
dist = distancia_punto_plano(plano, p4)
print(dist)

(array([0.57735027, 0.57735027, 0.57735027]), -0.5773502691896258)
1.154700538379252

Proyección ortogonal de un punto sobre una recta#

Dados:

  • una recta, definida por la tupla \((\mathbf{p_o}, \mathbf{v})\)

  • un punto \(\mathbf{p}\),

se desea calcular el punto proyección ortogonal \(\mathbf{p_r}\) de \(\mathbf{p}\) sobre la recta \((\mathbf{p_o}, \mathbf{v})\).

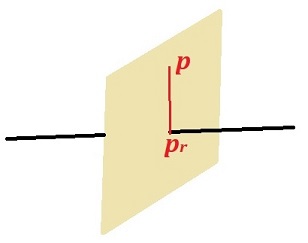
proyeccion_punto_recta.jpg

Con estos datos es inmediato obtener el plano perpendicular a la recta que pasa por el punto \(\mathbf{p}\), que vendrá dado por la tupla \((\mathbf{v}, D) = (\mathbf{v}, -\mathbf{p} \bullet \mathbf{v})\).

Finalmente, el punto \(\mathbf{p_r}\) buscado es la intersección de la recta \((\mathbf{p_o}, \mathbf{v})\) con el plano \((\mathbf{v}, D)\).

def proyeccion_punto_recta(recta, punto):
    '''
    Parameters
    ----------
    recta : tuple : (numpy.ndarray of floats, numpy.ndarray of floats)
        Recta definida por la tupla punto inicial y vector director:
        p=p_0+l*v
    punto : numpy.ndarray of floats
        Vector unidimensional representando 1 punto 3D
    Returns
    -------
    p_r : numpy.ndarray of floats
        El punto proyección sobre la recta
    Example
    -------
    >>> p1 = np.array((2, 2, 2))
    >>> p2 = np.array((3, 3, 3))
    >>> recta = recta_dos_puntos(p1, p2)
    >>> p = np.array((5, 1, 2))
    >>> p_r = proyeccion_punto_recta(recta, p)
    '''

    plano = (recta[1], -np.dot(recta[1], p))
    p_r = interseccion_recta_plano(recta, plano)

    return p_r

p1 = np.array((2, 2, 2))  
p2 = np.array((3, 3, 3))
recta = recta_dos_puntos(p1, p2)
p = np.array((-1, 0, 1))    
p_r = proyeccion_punto_recta(recta, p)
    
print(p_r)

[0. 0. 0.]
Contents