Funciones predefinidas#
Introducción
Funciones nativas
Funciones definidas en módulos
Introspección
Acceso a atributos. El operador punto: .
Conversiones de tipos
Introducción#
Las operaciones aritméticas elementales que hemos visto combinan valores y operadores para obtener un nuevo valor. No obstante, existen operaciones matemáticas que aún no hemos comentado a las que usualmente tenemos acceso en una calculadora comercial convencional. Ejemplos son la utilización de funciones matemáticas comunes, tales como la raíz cuadrada, potencias, funciones trigonométricas, logaritmos, etc.
Python, al igual que otros lenguajes de programación, tiene también el concepto de función, cuyo significado no coincide de forma exacta con la definición matemática, pero que puede ser utilizada para dar cuerpo a estas últimas.
Las funciones de Python serán objeto de un estudio más detallado posteriormente, donde aprenderemos a programar nuestras propias funciones. De momento, iremos introduciendo algunas de las funciones nativas (built-in functions) que Python pone a nuestra disposición.
Funciones nativas#
Un ejemplo de función numérica que está siempre a nuestra disposición es abs(), que se utiliza para hallar el valor absoluto de valores enteros o reales y el módulo de números complejos.
# Uso de la función abs()
abs(-1)
1
Nótese en la celda anterior el uso de comentarios: líneas de texto libre, que comienzan con el carácter # y que se extienden hasta el final de la línea. Estos comentarios son ignorados por el intérprete, pero son útiles para aclarar el funcionamiento del código.
La regla de estilo PEP 8 sugiere dejar un espacio en blanco tras
#
Las funciones pueden aparecer formando parte de expresiones más complejas.
# ¿Puedes predecir el resultado de la siguiente expresión?
10**abs(2*3 - 7) + 5
15
La expresión
10**abs(2*3 - 7) + 5
es interpretada por Python siguiendo las reglas de precedencia. Así, la potencia debe ser evaluada primero. Pero para hacerlo, el intérprete necesita primero obtener el valor absoluto de la subexpresión que está entre los paréntesis, los cuales forman parte de la sintaxis de la función. Los pasos serían:
Se evalúa la subexpresión
2*3 - 7, obteniéndose el valor-1. Este es el valor del parámetro que se envía a la funciónabs().La función
abs()devuelve el valor absoluto de-1, es decir,1.El valor devuelto
1es el exponente de la base10. El resultado es10.Al valor
10se le suma el operando5.
Otro ejemplo, es la función predefinida round(), que devuelve redondeada la expresión entre paréntesis al entero más cercano, 3 en el ejemplo:
round(3.1)
3
Las funciones en Python pueden diseñarse para recibir un número opcional de parámetros.
Así, la función round() puede ser utilizada con dos parámetros: el primero sigue siendo el número real a redondear, pero el segundo es un entero que especifica el número de lugares decimales para el redondeo. En este caso, el valor devuelto ya no es un entero sino un real.
# Prueba diferentes lugares decimales para el redondeo
round(3.14159, 3)
3.142
Un elemento importante de la sintaxis de los lenguajes de programación es que admiten la composición:
Cualquier subexpresión que participe en una expresión puede ser sustituida por otra subexpresión equivalente, originando una expresión resultante que será también sintácticamente correcta.
Esto incluye el uso de las funciones en las expresiones. Ya vimos antes que el valor del parámetro que se envía a una función puede ser el resultado de la evaluación de otra expresión.
Por ejemplo:
# ¿Cuál será el valor que resulta? ¿En qué orden serán llamadas las funciones?
abs(round(3.5) - 10)
6
Existen funciones predefinidas asociadas al trabajo con cadenas de caracteres (y de otras secuencias) que veremos a lo largo del curso. Por el ejemplo, la función len() devuelve un entero con el tamaño de la cadena, es decir, el número de caracteres que la forman, incluidos espacios en blanco, que son caracteres al fin y al cabo.
len("hola mundo ")
11
Funciones como abs(), round() o len() están predefinidas y directamente disponibles por el intérprete de Python. Existen otras muchas funciones nativas que iremos viendo poco a poco. Una lista completa de las mismas puede ser consultada en este enlace.
Funciones definidas en módulos#
Además de las funciones nativas del lenguaje existen muchas otras, útiles en diferentes campos, que están disponibles si se importa el módulo adecuado.
Una discusión más en profundidad del significado de los módulos, cómo trabajar con ellos y cómo crearlos se hará más adelante. Por ahora baste mencionar que mediante ellos podemos acceder a un conjunto suplementario de funciones.
Una forma de importar todas las funciones de un módulo es con la expresión:
from modulo import *
Por ejemplo, el modulo math contiene las habituales funciones matemáticas, cos(), exp(), log(), etc., funciones coincidentes con las de la biblioteca homónima del lenguaje C.
Un conjunto completo de las funciones del módulo math se encuentra en el siguiente enlace.
# ¿Puedes predecir el resultado antes de ejecutarlo?
from math import * # Importamos el módulo math
log(exp(cos(0)))
1.0
Aunque importar con la expresión from modulo import * puede resultar cómodo, lo cierto es que es totalmente desaconsejable. La razón es que diferentes módulos pueden contener identificadores coincidentes.
Por ejemplo, los módulos math y cmath (este último adaptado al cálculo con números complejos) tienen ambos una función para el cálculo de raíces cuadradas, sqrt().
En el ejemplo siguiente, al importarse en segundo lugar el módulo math se sobrescribe la función sqrt() para complejos y el cálculo produce un error en tiempo de ejecución ValueError. ¡Se ha producido una colisión entre identificadores!
from cmath import *
from math import *
sqrt(-3)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[8], line 4
1 from cmath import *
2 from math import *
----> 4 sqrt(-3)
ValueError: math domain error
Nótese que el hecho de que se produzca este error es una buena noticia. Imaginad una colisión entre dos funciones con desempeños diferentes que no generen este tipo de error. ¡Tendríamos un error semántico de difícil detección!
Si en la celda anterior cambiamos el orden de importación, el error desaparece. ¡Verifícalo!
Procedimiento de importación#
¿Cuál es la manera correcta de proceder? Veámoslo con el mismo ejemplo.
import cmath
import math
cmath.sqrt(-3)
1.7320508075688772j
Ahora, para acceder a las funciones de cada módulo anteponemos su nombre seguido del operador punto: ..
Es cierto que el código resultante es más verboso, pero evitamos colisiones entre los identificadores de los objetos definidos en cada módulo. Tanto cmath. como math. actúan como espacio de nombres (namespaces) que permiten acceder al correcto identificador contenido en cada módulo.
Introspección#
Ya hemos comentado que en Python, tanto las variables como las funciones son objetos. Entre las funciones nativas que proporciona Python se encuentran aquellas que permiten examinar las propiedades de un objeto en tiempo de ejecución.
La función type()#
La función type() interroga el tipo del valor de un objeto.
a = 1
type(a)
int
a = 1.1
type(a)
float
a = 'Hola'
type(a)
str
La función id() y el operador is#
La función nativa id() muestra por pantalla un entero, que es único para cada objeto almacenado en memoria.
x = 3.5
id(x)
2435265587152
y = x
id(y)
2435265587152
Nótese que la función id() devuelve la identificación del objeto float de valor 3.5. Las variables x e y son meras etiquetas ligadas a ese objeto.
El operador is permite determinar si dos variables están ligadas al mismo objeto.
x is y
True
La salida de la celda anterior es True. Es un resultado lógico o booleano (en referencia al álgebra de G. Boole). El otro posible valor es False. Hablaremos sobre este nuevo tipo de dato más adelante.
x = 5.6
x is y
False
Por otro lado, dos identificadores pueden estar asociados a objetos diferentes con el mismo tipo y valor. En el siguiente ejemplo, x e y tienen el valor 5000, pero, en cada caso, el objeto tipo int que almacena ese valor es diferente, se almacenan en memoria en lugares distintos.
x = 5000
y = 10000//2
x is y
False
Esto podría parecer un desperdicio de memoria. Sin embargo, para las relativas pocas ocasiones en que esto pueda ocurrir, hacer que el intérprete verifique cada vez que se crea un nuevo objeto si ya hay un objeto en memoria coincidente lo que sería es un desperdicio de tiempo.
x = 2
y = 10000//5000
x is y
True
En la celda superior, sin embargo, vemos que ambos enteros de valor 2 son almacenados en la misma zona de memoria. Esto es una característica de implementación interna de Python. Los valores enteros en el intervalo \([-5,256]\) son usados tan frecuentemente en los programas que están almacenados en una caché, precargados en memoria: de esta forma se ahorra tiempo y espacio.
La función dir()#
La función nativa dir() muestra por pantalla todos los atributos, datos y métodos, utilizables con un objeto.
a = 1.1
dir(a)
['__abs__',
'__add__',
'__bool__',
'__ceil__',
'__class__',
'__delattr__',
'__dir__',
'__divmod__',
'__doc__',
'__eq__',
'__float__',
'__floor__',
'__floordiv__',
'__format__',
'__ge__',
'__getattribute__',
'__getformat__',
'__getnewargs__',
'__getstate__',
'__gt__',
'__hash__',
'__init__',
'__init_subclass__',
'__int__',
'__le__',
'__lt__',
'__mod__',
'__mul__',
'__ne__',
'__neg__',
'__new__',
'__pos__',
'__pow__',
'__radd__',
'__rdivmod__',
'__reduce__',
'__reduce_ex__',
'__repr__',
'__rfloordiv__',
'__rmod__',
'__rmul__',
'__round__',
'__rpow__',
'__rsub__',
'__rtruediv__',
'__setattr__',
'__sizeof__',
'__str__',
'__sub__',
'__subclasshook__',
'__truediv__',
'__trunc__',
'as_integer_ratio',
'conjugate',
'fromhex',
'hex',
'imag',
'is_integer',
'real']
Acceso a atributos. El operador punto: .#
Para acceder a un atributo de un objeto, debe utilizarse el operador punto: ..
Ejemplos con complex
Por ejemplo, los valores de tipo complex tienen, entre otros, dos atributos llamados real e imag, que permiten acceder de forma individual a la parte real e imaginaria del valor.
a = 3.1 + 5.62j
a.real
3.1
a.imag
5.62
En el siguiente ejemplo, el método .conjugate() obtiene el complejo conjugado de a.
b = a.conjugate()
b
(3.1-5.62j)
Ejemplos con str
El método .upper() actúa sobre el valor de una variable de tipo str transformando todos sus caracteres a mayúsculas.
a = "cadena para probar métodos"
a.upper()
'CADENA PARA PROBAR MÉTODOS'
Obsérvese que un método es conceptualmente similar a una función en el sentido de que ejecuta un código que devuelve algún valor. A diferencia de una función convencional, el método está asociado al objeto sobre el que actúa.
Hay muchos otros métodos asociados a las cadenas: para una referencia completa puede consultarse en este enlace.
Algunos métodos útiles:
str.lower() # convierte a minúsculas los caracteres de la cadena.
str.capitalize() # hace que el primer carácter de la cadena esté en mayúscula.
str.title() # hace que todas las palabras comiencen con caracteres en mayúscula.
str.isalnum() # devuelve `True` si todos los caracteres de la cadena son alfanuméricos.
str.isdigit() # devuelve `True` si todos los caracteres son dígitos.
cad = "1232"
cad.isdigit()
True
Ejemplos para float
Para valores numéricos también disponemos de métodos. Por ejemplo, el método .as_integer_ratio() de los float devuelve la representación fraccionaria del número real.
a = 1.5
a.as_integer_ratio()
(3, 2)
El método .is_integer() devuelve True si el valor no tiene parte fraccionaria.
a = 2.0
a.is_integer()
True
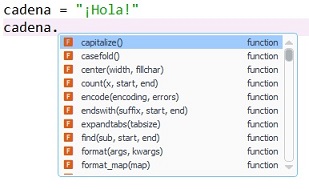
En el entorno Jupyter Notebook pulsando el tabulador después de escribir la variable y el operador punto,
variable., se muestra un menú desplegable que nos muestra los atributos y métodos asociados al tipo de objeto al que está asociada variable. En el caso de Spyder es aún más cómodo, pues se muestra automáticamente.
Conversiones de tipos#
Para determinados tipos, es posible realizar conversiones entre ellos. Existen diversas funciones de conversión de tipo: float(), int(), complex(), etc.
a = 23
b = float(a)
type(b)
float
Estas funciones de conversión de tipos son muy versátiles: pueden recibir como argumentos diferentes valores representando distintos tipos de datos. Son incluso capaces de convertir una cadena de caracteres, que puede representar un valor (entero en el ejemplo), al valor numérico equivalente. Como veremos en el próximo capítulo, esta capacidad de transformar de caracteres a enteros o reales es capital para introducir valores desde el exterior a nuestros programas o para mostrar los resultados obtenidos.
a = "1221"
int(a) # Se obtiene el entero representado en la cadena, si es posible
1221
Si la conversión no es posible, se genera una excepción.
a = "12.21"
int(a) # Se obtiene el entero representado en la cadena, si es posible
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[29], line 2
1 a = "12.21"
----> 2 int(a)
ValueError: invalid literal for int() with base 10: '12.21'
La función str() por su parte, recibe como argumento un valor y lo convierte a su representación como cadena de caracteres.
str(1.e-12)
'1e-12'
