Funciones#
Introducción
Definición de funciones
Tipos de funciones según sus parámetros y resultados devueltos
Parámetros y argumentos
Alcance de las variables: variables locales y globales
Funciones y tratamiento de excepciones
Proceso de desarrollo de un programa
Introducción#
En los temas previos ya hemos tenido oportunidad de trabajar con funciones. En este tema aprenderemos a definir y utilizar funciones creadas por nosotros.
A lo largo del tiempo y en diferentes lenguajes el concepto de función aparece definido también por otros nombres: subprograma, subrutina o procedimiento son los más habituales y con diferentes matices denotan lo mismo.
Una función es un conjunto de instrucciones al que se asigna un nombre, opcionalmente con parámetros de entrada y resultados de salida, y que puede ser llamada desde otras partes de un programa para realizar una tarea concreta.
La necesidad de las funciones#
Los lenguajes de programación utilizan los recursos que brinda el hardware del ordenador: la capacidad de codificar diferentes tipos de datos y la posibilidad de realizar sobre ellos operaciones aritméticas y lógicas.
Las operaciones que el ordenador realiza de forma nativa son bastante elementales y no van mucho más allá de:
la capacidad de realizar sumas, restas, multiplicaciones, divisiones y comparaciones.
controlar el flujo del programa modificando la ejecución secuencial de las sentencias mediante la utilización de condicionales y bucles.
De manera que la realización de todo el resto de complicadas operaciones que sabemos que son capaces de realizar los programas de ordenador deben ser construidas a partir de esas operaciones básicas.
Cuando utilizamos los operadores más sencillos en Python (suma, resta, etc.), el intérprete traduce los comandos de alto nivel dados por el programador y usa, casi directamente, las funcionalidades del hardware.
Por tanto, a la hora de hacer operaciones más complejas, estas tienen que ser creadas a partir de esos bloques elementales implementando procedimientos más elaborados. Python y otros lenguajes ofrecen la posibilidad de agrupar estos bloques de instrucciones en forma de una función, para su posterior invocación de forma sencilla.
Un ejemplo usando funciones de biblioteca#
Ya hemos utilizado muchas funciones, algunas nativas y otras disponibles en módulos, como math.
Por ejemplo, supongamos que queremos determinar el siguiente cociente:
El cálculo de \(y\) se podría implementar en Python con un programa como el siguiente, que hace uso de las funciones trigonométricas sin() y cos() definidas en el módulo math:
# Desaconsejado usar import *, pero utilizado aquí para argumentar el uso de funciones
from math import *
x = pi
y = (1 - sin(x/4)*cos(x)**4)/(1 + cos(x)**2)
print(y)
0.1464466094067262
Se debe resaltar lo siguiente en el ejemplo anterior:
Claridad
Observad la similitud en el uso (que no equivalencia) para este caso concreto de las funciones en Python con el concepto matemático de función. La función recibe valores como parámetros y devuelve un resultado que entonces participa en la evaluación del resto de la expresión.
Abstracción
Como usuarios de las funciones
sin()ycos()no sabemos cómo están implementadas. Podríamos aventurar que es posible que la implementación de las mismas recurra a la expansión de series que converjan a las funciones requeridas, con una precisión alta pero finita. Pero el hecho cierto es que no lo sabemos, y tampoco nos interesa para utilizarlas: evidentemente hay que dar un salto de fe y confiar en que sean correctas dentro de los límites de la precisión que aseguran.Reutilización
Hemos utilizado dos veces la función
cos()y una elsin(). Podemos imaginar que utilizar más expresiones, usando estas funciones un número mayor de veces, no implicaría una dificultad mucho mayor.
Imaginemos, por el contrario, que las funciones no existieran. Y que cada vez que quisiéramos determinar el seno o coseno de un número, tuviésemos que programar los bucles y condicionales del algoritmo específico que determina el valor de estas funciones a partir de operaciones más básicas. Ciertamente, sería muy complicado resolver cualquier problema matemático sencillo. El código resultante sería enormemente difícil de entender. Por otra parte, si se decidiera cambiar la implementación del código, para utilizar otro algoritmo más preciso o eficiente, eso implicaría modificar todo el programa.
Una vez visto el ejemplo, mostramos ahora la forma recomendada de usar funciones importadas de un módulo.
import math
x = math.pi
y = (1 - math.sin(x/4)*math.cos(x)**4)/(1 + math.cos(x)**2)
print(y)
0.1464466094067262
Ventajas del uso de funciones#
Las funciones presentan dos beneficios importantes de los que se pueden derivar muchos otros:
Estructura: es un recurso que permite descomponer una tarea compleja en varias subtareas de menor entidad, que puedan ser abordables con mayores garantías de éxito.
Abstracción: las funciones ocultan detalles tras una interfaz pública bien definida. Se hace abstracción de los detalles de implementación y lo que interesa únicamente son los valores de entrada que se le suministran y los resultados que devuelve.
A partir de estas dos características básicas, se derivan el resto de las ventajas que del uso de las funciones:
Permiten reutilizar código sin tener que reescribirlo cada vez.
Posibilitan el encapsulamiento del código de la función. Así, por ejemplo, una vez dado por válido el código interno de una función, los errores de un programa no serán imputables a la implementación interna de la función.
La implementación interna puede cambiar sin que el programador que use esas funciones tenga que preocuparse de ello.
Hace que el código resultante sea más claro y mantenible.
Las funciones brindan el mecanismo para dividir un problema grande en subproblemas pequeños, acotando la interacción entre los mismos a los datos intercambiados a través de su interfaz pública.
Es el mecanismo ideal para permitir la colaboración entre varios programadores: una vez puestos de acuerdo en la interfaz, cada cual tiene la libertad de programar la solución a los subproblemas parciales sin temor a que le afecte lo hecho por otros programadores (siempre que el resultado facilitado sea el correcto).
Pautas de diseño de una función#
Las características que deben prevalecer a la hora de diseñar una función son aquellas que refuerzan el hecho de que las funciones son abstracciones.
Una función como abstracción debe centrarse en 3 propiedades:
Su dominio, conjunto de valores que pueden tomar sus parámetros de entrada.
Su rango, conjunto de valores que puede devolver como resultado.
Su propósito, la relación existente entre los valores de entrada y los de salida, así como los posibles efectos colaterales que puedan existir.
Cómo se logran las salidas a partir de las entradas queda oculto, ese es el mecanismo de la abstracción.
Para lograr reforzar el mecanismo de abstracción de una función hay algunas pautas que son de ayuda:
Cada función debe tener un único propósito. Es el principio de responsabilidad única.
El objetivo perseguido con la función debería ser fácilmente identificado con un nombre corto.
Si una función hace múltiples tareas de forma consecutiva, debería rehacerse en múltiples funciones.
No te repitas (DRY, Don’t repeat yourself).
Si un fragmento de código aparece varias veces repetido, es una buena oportunidad para darle un nombre e invocarlo múltiples veces.
Las funciones deben ser generales.
No tiene sentido, por ejemplo, definir una función específica para elevar un número a la quinta, cuando podemos definir con carácter general, una función que eleve un número a cualquier exponente.
Definición de funciones#
Al acto de utilizar una función, tal y como hemos venido haciendo hasta ahora con las funciones nativas (built-in) y también con las de biblioteca, se le conoce con el nombre de llamar o invocar a la función.
Aprenderemos a continuación cómo definir nuestras propias funciones con algunos ejemplos sencillos.
# Primero definimos la función, especificando su nombre y sus parámetros
def area_circulo(r):
'''Función que recibe el radio del círculo y calcula su área'''
area = 3.1415*r**2
return area
# El estilo PEP 8 recomienza dejar dos líneas en blanco después de una función
diametro = 10
area = area_circulo(diametro/2)
print(f'El área del círculo de diámetro {diametro} es {area}.')
El área del círculo de diámetro 10 es 78.53750000000001.
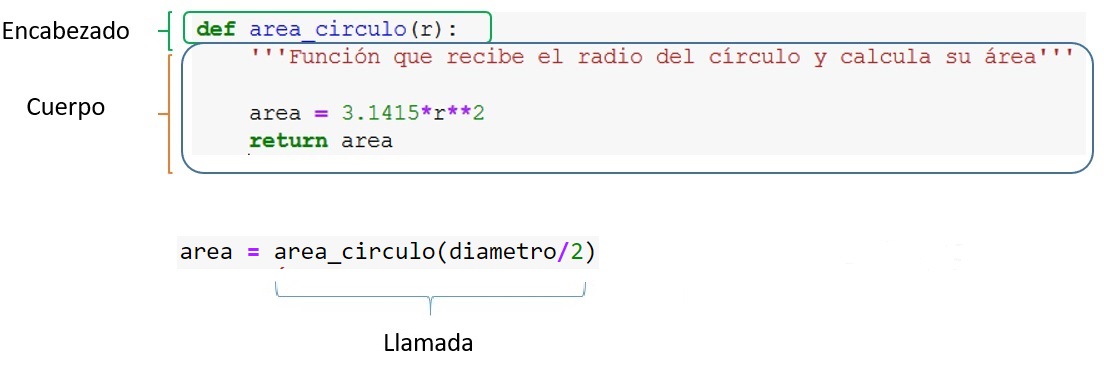
Observe en lo anterior los dos momentos del trabajo con las funciones, la definición y la llamada:
Definición:
def area_circulo(r): '''Función que recibe el radio del círculo y calcula su área''' area = 3.1415*r**2 return area
Debe aparecer antes de la primera llamada y está formada por dos partes, el encabezado y el cuerpo:
Encabezado:
def area_circulo(r):
Se utiliza la palabra reservada
defseguida del identificador que da nombre a la función,area_circuloen el ejemplo. Le sigue entre paréntesis (obligatorios) la lista de parámetros, que puede estar vacía. En el ejemplo, consta de un solo parámetro al que hemos identificado dentro de la definición de la función con el nombrer.Note que, al definir la función, todavía no se ejecuta el código que ella representa, aunque aparezca primero dentro de la secuencia del programa.
Cuerpo:
area = 3.1415*r**2 return area
Después del encabezado, se tiene el cuerpo de la función. Se debe notar que, de nuevo, Python exige el sangrado apropiado para identificar el cuerpo de la función.
La primera sentencia asigna a la variable
areael resultado de evaluar la expresión a su derechaLa segunda sentencia utiliza la palabra reservada
returnpara devolver el contenido deareaal código que haya invocado a la función.
Es importante entender que
areadentro de la definición de la función da nombre a una variable local que solo está definida y accesible dentro de la funciónarea_circulo(). El identificadorrigualmente solo está definido dentro de la función.Entre triples comillas,
'''texto''', que es otro estilo de comentario, hemos documentado brevemente el objeto de la función.Llamada(s):
area = area_circulo(diametro/2)
Se realiza escribiendo el nombre de la función, seguido obligatoriamente de los paréntesis con los argumentos (en este caso uno) que se le pasarán a la misma. Aquí el argumento se obtiene evaluando la expresión indicada,
diametro/2.
A tener en cuenta:
Antes de llamar a una función, ésta debe haber sido definida previamente en el programa.
La primera sentencia útil que se ejecuta es la primera sentencia del programa principal. Programa principal es el conjunto de todas las sentencias que no están incluidas dentro del cuerpo de ninguna función.
Si la función tiene parámetros de entrada, a la hora de llamar a la función se calculan los valores de los argumentos, evaluando las expresiones correspondientes (en el ejemplo se evalúa
diametro/2). El valor del argumento resulta asociado al parámetro de la función (en este casor).
En el siguiente ejemplo, que calcula el área de un cilindro, vemos una reutilización de la función area_circulo(r).
# Programa principal
radio = float(input("Diga el radio: "))
altura = float(input("Diga la altura: "))
area_cilindro = 2*area_circulo(radio) + 2*3.1415*radio*altura
print(f'El área de un cilindro de radio {radio} y altura {altura} es {area_cilindro}.')
Las sentencias que se ejecutarán primero de forma secuencial corresponden al programa principal:
la asignación a las variables
radioyalturade los valores que el usuario introduzca por tecladola evaluación de la expresión que se asigna a una nueva variable,
area_cilindro. Como la funciónarea_circulo()devuelve un valor, la llamada a dicha función puede participar de la expresión en la que se calcula el área lateral del cilindro. Nótese que esta forma de utilizar la función que acabamos de definir, no difiere de lo ya visto en temas anteriores o del ejemplo del inicio de este documento con las funciones de bibliotecacos()ysin().la salida por pantalla de los resultados
Al evaluar la expresión en la que aparece la llamada a area_circulo(), se procede siguiendo las reglas de precedencia de los operadores implicados. Primero, cuando se intenta realizar el primer producto, el intérprete de Python comprende que necesita antes evaluar la función area_circulo(), con lo que se detiene la evaluación de la expresión para invocar a la función, asociando el contenido del argumento radio al parámetro r de la definición de la función. Tras terminar la ejecución, la función devuelve el valor del área del circulo contenida en la variable local area, y dicho valor es recibido en el programa principal para proceder con la evaluación del resto de la expresión.
Nótese que area_circulo() tiene un comportamiento similar a las funciones matemáticas: a cada valor del dominio de definición (cada valor del parámetro r) le corresponde un único valor de la imagen (la salida que se logra mediante la sentencia return) y, además, este valor siempre es el mismo.
Principios de responsabilidad única y de generalidad#
Desde el punto de vista de la ingeniería del software es deseable que una función realice una única labor, lo que podría enmarcarse dentro de lo que se conoce como principio de responsabilidad única.
Veamos un ejemplo de diseño de función desafortunado:
def area_circulo_desafortunado(r):
area = 3.1415*r**2
print("Área del círculo de radio {} es {}.".format(r, area))
return area
Esta función tiene dos responsabilidades: calcular el área de un círculo e imprimir su valor por pantalla.
A la hora de programar funciones, se debe buscar que éstas sean lo más generales posible, de forma que puedan ser reutilizadas en diferentes circunstancias. La función anterior no es muy flexible, puesto que siempre imprime en pantalla el resultado y, probablemente, no en todas las ocasiones ese es el comportamiento que se desea.
Por tanto, desde otro punto de vista, violaría un principio de generalidad: no en todos los casos en que se quiera calcular el área del círculo, se desea imprimir el resultado por pantalla. Más bien lo contrario.
Tipos de funciones según sus parámetros y resultados devueltos#
Funciones sin parámetros de entrada#
def intro():
print('Este código solo imprime este mensaje.')
intro()
intro()
Este código solo imprime este mensaje.
Este código solo imprime este mensaje.
Las funciones pueden carecer de parámetros de entrada. Observe que el único objetivo en este caso es sacar un aviso por pantalla.
Puede existir una función trivial, que no hace nada.
def funcion():
pass # TODO: completar más tarde
En todo caso, los paréntesis deben ser obligatoriamente utilizados tanto en la definición como en cada una de las llamadas a la función.
La sentencia pass#
La palabra clave pass indica algo así como no hacer nada. Suele utilizarse en ocasiones para crear la estructura de un programa sin que sea necesario tener completado todo su código.
Funciones que no devuelven valores#
El caso del ejemplo anterior también ejemplifica a las funciones que no contienen la sentencia return.
Este tipo de funciones devuelven el valor especial None, que indica la ausencia de un valor válido.
Por ejemplo:
a = intro()
print(a)
Este código solo imprime este mensaje.
None
Funciones con más de un parámetro#
Las funciones pueden tener más de un parámetro. Tomando como referencia el ejemplo ya visto, definamos una función que reciba el radio y la altura de un cilindro y devuelva su área.
# Primero definimos la función, especificando su nombre y sus parámetros
def area_cilindro(r, h):
'''Función que recibe el radio y la altura de un cilindro y calcula su área'''
pi = 3.14159
area = 2*pi*r**2 + 2*pi*r*h
return area
radio = 1
altura = 4.5
area_c = area_cilindro(radio, altura)
print(f'El área del cilindro de radio {radio} y altura {altura} es {area_c}.')
El área del cilindro de radio 1 y altura 4.5 es 34.55749.
Note que los parámetros de area_cilindro() ahora son dos, representando el radio (r) y la altura (h).
Obsérvese la correspondencia posicional entre los parámetros y los argumentos: la variable radio se ligará al primer parámetro, r, y la variable altura al segundo, h.
Funciones que devuelven más de un resultado#
En Python, las funciones pueden devolver mediante la sentencia return un número arbitrario de valores separados por coma, es decir, agrupándolos en una tupla (en sentido estricto se devuelve un único valor). Esto representa una potente característica del lenguaje que lo diferencia de otros que no lo poseen de forma tan directa, como el C/C++.
Por ejemplo:
def min_max(lista):
'''Devuelve el mínimo y el máximo de la lista que recibe como argumento'''
mn = mx = lista[0]
for elem in lista[1:]: # [1:] evita comparar con el índice 0
if mn > elem:
mn = elem
elif mx < elem:
mx = elem
return mn, mx # Devolvemos una tupla
lista_prueba = [1, 10, 2, -3, 6, 8]
mn, mx = min_max(lista_prueba) # Desempaquetado de la tupla
print(f'Los valores extremos de la lista {lista_prueba} son:\nMin: {mn} Max: {mx}')
Los valores extremos de la lista [1, 10, 2, -3, 6, 8] son:
Min: -3 Max: 10
Observe que, en el ejemplo anterior, el parámetro que espera la función min_max() es de tipo list. Este ejemplo, además, ilustra bien el hecho de que las funciones deben ser entendidas como subprogramas, capaces de utilizar todas las posibilidades vistas: definir sus propias variables, utilizar estructuras de control de flujo como condicionales y bucles, etc.
La sentencia return devuelve el mínimo y máximo valor de la lista de entrada, creando una tupla.
En la línea en que se realiza la llamada, se asigna el resultado a dos variables, desempaquetando la tupla.
Especificando el nombre de los parámetros#
Python permite especificar los nombres de los parámetros a la hora de invocar a la función.
area_c = area_cilindro(1, h=4.5)
print("El área del cilindro es", area_c)
El área del cilindro es 34.55749
area_c = area_cilindro(r=1, h=4.5)
print("El área del cilindro es", area_c)
El área del cilindro es 34.55749
Para evitar ambigüedades, en la llamada no se permite que un argumento que no tenga nombre, argumento posicional, esté a la derecha de un argumento con nombre.
area_c = area_cilindro(r=1, 4.5)
print("El área del cilindro es", area_c)
Cell In[12], line 1
area_c = area_cilindro(r=1, 4.5)
^
SyntaxError: positional argument follows keyword argument
Poder especificar nombres permite que los argumentos pueden ser enviados a la función en cualquier orden.
area_c = area_cilindro(h=4.5, r=1)
print("El área del cilindro es", area_c)
El área del cilindro es 34.55749
Parámetros con valores por defecto#
En ocasiones resulta útil definir funciones para las que uno o varios parámetros tengan valores por defecto.
Supongamos, por ejemplo, que hacemos una función para garantizar que el valor que se pasa como argumento está entre dos límites dados:
si lo está, devuelve el valor tal cual.
si no lo está, devuelve el límite superior o inferior, según el caso.
Se sabe además que, en la aplicación de que se trata, el rango de valores que interesa normalmente suele ser el [0,1]. Una implementación posible de dicha función es la que se muestra:
def limita(valor, inf=0., sup=1.):
'''Devuelve valor si inf < valor < sup.
Si valor < inf devuelve inf.
Si valor > sup devuelve sup'''
if inf <= valor <= sup:
return valor
elif valor > sup:
return sup
else:
return inf
valor = 3.
# con límites por defecto
print(f'Valor {valor} limitado en el rango por defecto [0.0, 1.0]: {limita(valor)}')
# con un límite cambiado: inf -> -1.
print(f'Valor {valor} limitado en el rango [-1.0, 1.0]: {limita(valor, -1.)}')
# con un límite cambiado: sup -> 5.
print(f'Valor {valor} limitado en el rango [0.0, 5.0]: {limita(valor, sup=5.)}')
# con los dos límites cambiados: inf -> -1., sup -> 5.
print(f'Valor {valor} limitado en el rango [-1.0, 5.0]: {limita(valor, -1., 5.)}')
Valor 3.0 limitado en el rango por defecto [0.0, 1.0]: 1.0
Valor 3.0 limitado en el rango [-1.0, 1.0]: 1.0
Valor 3.0 limitado en el rango [0.0, 5.0]: 3.0
Valor 3.0 limitado en el rango [-1.0, 5.0]: 3.0
Observe que, en el encabezado de la definición de la función, a los parámetros inf y sup se les asignan respectivamente los valores 0.0 y 1.0. Esto significa que, si a esos parámetros no se les pasa un valor durante la llamada a la función, se utilizarán en el cuerpo de la misma esos valores por defecto.
En la tercera llamada a la función, se requiere cambiar el límite superior solamente. Para estos casos, se puede utilizar una llamada a función que utiliza, no la posición del argumento como criterio de emparejamiento, sino utilizar directamente el nombre del parámetro y el signo = para pasar el argumento. De no hacerlo así, y utilizar el paso posicional, habría que haber utilizado una llamada a función como la que se muestra a continuación, perdiendo la ventaja de los parámetros por defecto:
limita(valor, 0, 5)
Parámetros y argumentos#
En los apartados anteriores hemos establecido una clara diferencia entre los términos parámetro y argumento, que con frecuencia aparecen usados como sinónimos. A los primeros a veces se les denomina parámetros formales y a los segundos parámetros reales en otros lenguajes.
los argumentos se utilizan en las llamadas a las funciones
los parámetros son internos a las funciones y reciben inicialmente los valores de los argumentos.
Paso por referencia a objeto#
Como ya hemos comentado, las variables en Python son identificadores que referencian a objetos almacenados en bloques de memoria.
En el mecanismo de llamada a una función se relaciona típicamente una variable correspondiente a un argumento con una variable correspondiente a un parámetro. El mecanismo que subyace en esta asociación entre argumento y parámetro es el de que la variable parámetro pasa a estar ligada al mismo objeto al que referencia la variable argumento. Por ello, este mecanismo se conoce como paso por referencia a objeto.
En definitiva, el mecanismo es idéntico al que ocurre en una asignación: parametro = argumento. La particularidad es que los parámetros son locales a la función.
La siguiente celda ilustra claramente el mecanismo. La variable num referencia a un objeto con valor entero 3.
Tras la llamada, ambas variables están ligadas al mismo objeto, como prueba la función id().
def square(x):
print(f'Dentro de la función: x = {x}, id = {id(x)}')
return x**2
num = 3
print(f'Antes de la llamada: num = {num}, id = {id(num)}')
z = square(num)
Antes de la llamada: num = 3, id = 140718366102376
Dentro de la función: x = 3, id = 140718366102376
Este mecanismo es muy efectivo puesto que ahorra crear un nuevo objeto en memoria para el parámetro, copia del correspondiente al argumento. Esta nueva creación es lo que ocurre en otros lenguajes en el mecanismo de paso por valor, donde se crea un nuevo objeto en memoria, copia del pasado como argumento.
Veamos lo que ocurre en la siguiente celda:
def square(x):
print(f'Dentro de la función: x = {x}, id = {id(x)}')
x = x**2
print(f'Dentro de la función tras asignación: x = {x}, id = {id(x)}')
return x
num = 3
print(f'Antes de la llamada: num = {num}, id = {id(num)}')
z = square(num)
Antes de la llamada: num = 3, id = 140718366102376
Dentro de la función: x = 3, id = 140718366102376
Dentro de la función tras asignación: x = 9, id = 140718366102568
La sentencia x = x**2 crea un nuevo objeto, en el ejemplo de valor 9, al que pasa ahora a estar ligada la variable local x. No es sino una consecuencia del carácter inmutable de los tipos int, entre otros.
Parámetros mutables#
Los parámetros de la función, y las variables creadas en el cuerpo de la misma, son variables locales a dicha función y solo pueden ser accedidas desde código definido en el cuerpo de la misma en sentencias posteriores a su creación.
Esto parece contradecir lo que ocurre en el siguiente ejemplo, que usa como parámetro una lista. En este caso, la aparente variable local lista afecta a la variable externa enteros:
def square_lista(lista):
print(f'Dentro de la función, antes de realizar cálculos: lista = {lista}, id = {id(lista)}')
for i, x in enumerate(lista):
lista[i] = x**2
print(f'Dentro de la función, después de realizar cálculos: lista = {lista}, id = {id(lista)}')
enteros = [1, 3, 5, 2, 4]
print(f'Antes de la llamada: enteros = {enteros}, id = {id(enteros)}')
square_lista(enteros)
print(f'Después de la llamada: enteros = {enteros}, id = {id(enteros)}')
Antes de la llamada: enteros = [1, 3, 5, 2, 4], id = 2493765038592
Dentro de la función, antes de realizar cálculos: lista = [1, 3, 5, 2, 4], id = 2493765038592
Dentro de la función, después de realizar cálculos: lista = [1, 9, 25, 4, 16], id = 2493765038592
Después de la llamada: enteros = [1, 9, 25, 4, 16], id = 2493765038592
¡Vemos que se cumple el paso por referencia a objeto! El argumento enteros y el parámetro lista antes, durante y después de la llamada referencian al mismo objeto. Sin embargo, dentro de la función se han modificado sus elementos. Se ha producido un efecto colateral, en el que la función modifica objetos externos a ella.
Esto es una consecuencia del carácter mutable de las listas. En realidad, lo que ocurre es que una variable de tipo list
es un objeto compuesto de objetos. El bloque de memoria asociado al objeto contenedor original permanece inalterado, pero las referencias internas a sus elementos, que son objetos enteros inmutables, cambian necesariamente.
Para ver mejor lo que ocurre, la siguiente figura representa con fondo naranja varios objetos: un objeto tipo list y objetos tipo int, que son elementos de la lista y que pueden referenciarse a través del operador de indexación lista[i]. El mecanismo del objeto tipo list para acceder a sus elementos se representa en la figura de forma abstracta con los cuadrados de fondo azul.
La situación justo tras la llamada a la función es la siguiente, donde ambas variables tipo lista referencian al mismo objeto en memoria:
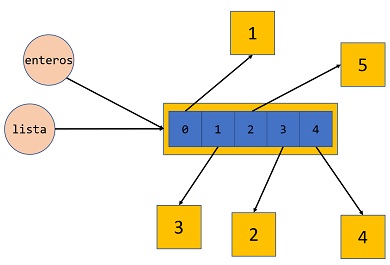
Antes de la abandonar la función square_lista(lista), la situación pasa a ser la siguiente:
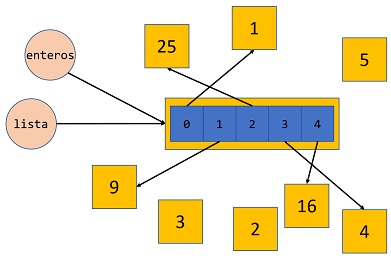
Se crean nuevos objetos int, 9, 16 y 25 y otros ¡son reutilizados!, como los objetos 1 y 4. Los objetos int 2, 3 y 5 ya no están ligados a lista, pero podrían estarlo a otras variables del programa.
Veamos en el ejemplo lo que ha ocurrido con las identidades de los elementos de la lista:
def square_lista(lista):
for i, x in enumerate(lista):
print(f'\nEl elemento {i} de la lista está asociado antes al objeto con dirección {id(lista[i])}')
lista[i] = x**2
print(f'después al objeto con dirección {id(lista[i])}')
enteros = [1, 3, 5, 2, 4]
square_lista(enteros)
El elemento 0 de la lista está asociado antes al objeto con dirección 140718366102312
después al objeto con dirección 140718366102312
El elemento 1 de la lista está asociado antes al objeto con dirección 140718366102376
después al objeto con dirección 140718366102568
El elemento 2 de la lista está asociado antes al objeto con dirección 140718366102440
después al objeto con dirección 140718366103080
El elemento 3 de la lista está asociado antes al objeto con dirección 140718366102344
después al objeto con dirección 140718366102408
El elemento 4 de la lista está asociado antes al objeto con dirección 140718366102408
después al objeto con dirección 140718366102792
Funciones puras e impuras#
Las funciones de Python que tienen un comportamiento similar a las funciones matemáticas, esto es, constituyen una relación unívoca entre el dominio de los valores de entrada y el valor de la salida, se denominan funciones puras.

Se puede decir de las funciones puras que:
Devuelven el mismo resultado al ser llamadas con los mismos argumentos de entrada.
El resultado solo depende de la entrada: no tienen memoria, no conservan un estado que les permita recordar que la misma ha sido invocada antes, para entonces devolver un valor distinto en llamadas sucesivas.
No tiene efectos colaterales (side effects). La única forma de interacción con el resto de programa, o el contexto en que éste se desarrolla, es a través de la sentencia
return. En especial:No modifican variables externas a la función.
No imprimen nada por pantalla, ni interaccionan de ninguna otra manera con el mundo exterior.
Las funciones impuras son el resto de las funciones, entre ellas aquellas que modifican los argumentos que sean mutables.
Ventajas de las funciones puras#
El trabajar preferentemente con funciones puras está en la base del paradigma funcional de programación, que en los últimos años está recobrando un nuevo auge.
El uso de funciones puras permite utilizar en programación las herramientas de análisis de las matemáticas y demostrar, en el sentido matemático del término, la corrección de un programa de ordenador. En cualquier caso, una descripción de los principios y prácticas de la programación funcional está fuera del ámbito de este curso introductorio.
Eso no impide que recomendemos, siempre que sea razonable, el uso funciones puras:
Al desaparecer los efectos colaterales, los programas son más fácilmente depurables.
Permite además la composición de funciones: el pasar como argumentos de funciones, directamente el valor devuelto por otra función (con cualquier grado de anidamiento). Ejemplo:
cos(log(x)).
La función square_lista(lista) podría fácilmente volver a implementarse como una función pura:
def square_lista_pura(lista):
'''Se recibe una lista y se devuelve una lista con los elementos de la original elevados
al cuadrado. La lista original no sufre modificación'''
lista_salida = [0]*len(lista)
for i, x in enumerate(lista):
lista_salida[i] = x**2
return lista_salida
enteros = [1, 3, 5, 2, 4]
lista_salida = square_lista_pura(enteros)
print(enteros, '\n', lista_salida)
[1, 3, 5, 2, 4]
[1, 9, 25, 4, 16]
El carácter puro cuando se usan argumentos mutables es un acto de fe. Salvo que nos aseguremos mediante la inspección del código, solo nos queda confiar en la documentación de la función al respecto.
La versión que vemos a continuación es un ejemplo de un error de principiante típico:
def square_lista_fallida(lista):
lista_salida = lista
for i, x in enumerate(lista_salida):
lista_salida[i] = x**2
return lista_salida
enteros = [1, 3, 5, 2, 4]
lista_salida = square_lista_fallida(enteros)
print(enteros, '\n', lista_salida)
[1, 9, 25, 4, 16]
[1, 9, 25, 4, 16]
Debemos recordar que las sentencias del tipo lista_salida = lista no crean un nuevo objeto. Crean una nueva referencia al objeto original, pero el objeto es el mismo.
Sin embargo, en la versión pura, lista_salida = [0]*len(lista) crea un objeto tipo list totalmente diferente.
Otra alternativa podría haber sido utilizar una notación especial de los cortes de listas:
def square_lista_pura_v2(lista):
lista_salida = lista[:]
for i, x in enumerate(lista_salida):
lista_salida[i] = x**2
return lista_salida
Finalmente, una forma elegante y pitónica de sustituir a esta función hubiese sido usar simplemente una lista por comprensión:
lista_salida = [x**2 for x in enteros]
Las funciones impuras son inevitables#
El objetivo de la programación es aceptar datos del mundo exterior, procesarlos de alguna forma y devolverlos al usuario. O sea, la utilidad global de los programas está precisamente en lograr determinados efectos colaterales.
En todo caso, resulta útil, confinar estás interacciones con el mundo exterior a determinadas funciones bien localizadas.
Ejemplos de funciones impuras imprescindibles o útiles:
Las funciones de entrada y salida, utilizando la consola, ficheros o redes informáticas, entre otras. Por ejemplo, la función
input(), aunque sea llamada con el mismo parámetro de entrada, puede devolver cada vez valores diferentes: el usuario humano tiene un estado o memoria.Función que devuelve un número aleatorio: resulta útil porque precisamente tiene memoria: devuelve un valor diferente cada vez.
Alcance de las variables: variables locales y globales#
El alcance de una variable da cuenta de las reglas que especifican desde qué sentencias del código Python son accesibles cada una de las variables, teniendo en cuenta el lugar dentro del código en el que han sido especificadas.
Como se ha visto, los parámetros de la función y las variables creadas en el cuerpo de la misma son variables locales a dicha función y solo pueden ser accedidas desde código definido en el cuerpo de la misma en sentencias posteriores a su creación.
Marcos de variables#
Al inicio de cada llamada a una función se crea internamente un marco de memoria local de valores que contiene:
los valores de entrada de los argumentos de la función
todas aquellas variables que la función declare localmente
El marco de memoria de la función estará vigente mientras el hilo de ejecución de la función se encuentre dentro de la misma, es decir, mientras la función no haya finalizado.
La esencia de una buena programación procedural y modular, y de ello la gran ventaja del uso de las funciones, reside precisamente en el uso preferente de variables locales, puesto que este es el mecanismo del lenguaje que brinda el grado apropiado de desacople necesario entre el código que usa una función y su implementación interna. Esto es, garantiza la muy necesaria abstracción que hace que podamos utilizar las funciones sin preocuparnos de los detalles internos.
Obsérvese que esta independencia quedaría destruida si las variables internas pudieran ser modificadas o accedidas externamente. De nuevo hay que recalcar que la interacción legítima con las funciones debe ser a partir de su interfaz pública: los parámetros y los valores de retorno.
# Multiplica n*10
def mult_10(n):
a = 10*n
print('a en mult_10: ', a, '\nn en mult_10: ', n)
return a
# Programa principal
a = 5
n = mult_10(3*a)
print('a en prog. principal: ', a, '\nn en prog. principal: ', n)
a en mult_10: 150
n en mult_10: 15
a en prog. principal: 5
n en prog. principal: 150
En el código previo, las variables a y n, creadas en el programa principal, no son las mismas que las variables con idéntico nombre en la función mult_10(). Estas últimas están definidas en el marco local de la función: la primera n es el nombre del parámetro de la función y la segunda es creada cuando se realiza la asignación a = 10*n. De hecho, debe notarse que, al llamar a la función, lo que se pasa como argumento a la misma, es el resultado de multiplicar 3*a. Finalmente, cuando la función retorna, es el valor de la variable local a el que resulta asignado a la variable n.
Este grado de desconexión entre las variables locales de las diferentes funciones y las del programa principal es precisamente lo que se busca. Nótese que la interpretación a efectos de legibilidad de la celda anterior puede ser un quebradero de cabeza. Pero, en condiciones normales, el usuario de una función no tiene acceso a su código interno, por lo que, en realidad, no tiene por qué existir ese problema.
Jerarquía de acceso a los nombres#
Acceso desde una función a una variable externa a su marco#
Si tenemos una función definida dentro del fichero principal, es cierto que desde la función se puede acceder a variables definidas en el programa principal, siempre que no haya ningún parámetro o variable local con el mismo nombre.
def func(b):
c = 30*a
print('func a =', a, 'b =', b, 'c =', c)
# Programa principal
a = 5
b = 10
c = 20
func(1)
print('Prog. principal a =', a, 'b =', b, 'c =', c)
func a = 5 b = 1 c = 150
Prog. principal a = 5 b = 10 c = 20
Se observa que desde la función se puede leer la variable a utilizada en el programa principal. Y la única razón de que no se pueda acceder a las variables b y c también del programa principal, es que el parámetro b y la variable local c tienen el mismo nombre.
Este ejemplo que acabamos de ver es una muestra de pésima programación, pues perdemos el encapsulamiento del código y la mantenibilidad del código se hace imposible.
Para comprender mejor este mecanismo, en Python se cumple una jerarquía de acceso a los nombres que se evidencia en el siguiente esquema.
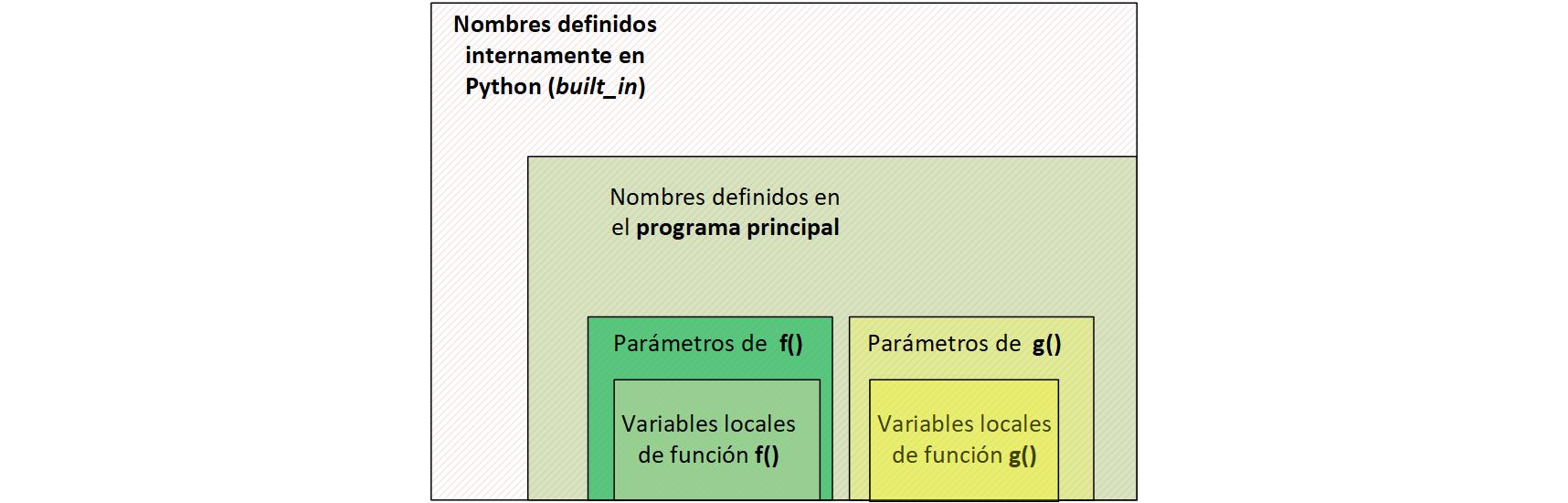
Esto es: si se produce una referencia a una variable de nombre dado en la función f(), Python determinará a quien se hace referencia, en el sentido en que se muestra en el esquema anterior:
primero comprobará si existe una variable local de
f()con ese nombreen caso de fallar, entonces se verá si se trata de un parámetro
si no lo es, se mirará si es una variable del programa principal, variables a las que podemos calificar de globales.
y finalmente si esto también falla, se intentará encontrar ese identificador entre los definidos intrínsecamente (built_in) en el lenguaje
si también esto falla, se producirá un error de tiempo de ejecución
Nótese que en la secuencia descrita de búsqueda para la variable a la que se hace referencia, no se menciona a la función g() que estaría definida al mismo nivel que f() y, por tanto, no participaría en la búsqueda de los nombres de esta función f().
En la siguiente celda, se intenta modificar dentro de la función func() la variable global a creada en el programa principal. A estas alturas ya sabemos que el efecto no es el pretendido.
def func():
a = 30
print('func a = ', a)
# Programa principal
a = 5
func()
print('Prog. principal a = ', a)
func a = 30
Prog. principal a = 5
Tal y como hemos visto, en la línea 2, Python crea de forma transparente al usuario una nueva variable con el mismo nombre pero local a func(). Por lo que, si la intención del programador era modificar la variable global a, no lo ha conseguido.
Variables globales#
Normalmente, no se debe acceder a variables globales desde dentro de las funciones: no es buena idea leer el valor de dichas variables, pero mucho menos modificarlas mediante una asignación. Un código en el que desde diferentes funciones se modifiquen variables globales es un programa de difícil mantenimiento y depuración.
Si existiera la necesidad puntual de modificar la variable global, en el ejemplo, ¿hay alguna forma?
La respuesta es que sí. Para ello hay que declarar dentro de la función la variable en cuestión como global. El siguiente código muestra cómo hacerlo.
# No hagas esto nunca
def func():
global a
a = 30
print('func a =', a)
# Programa principal
a = 5
func()
print('Prog. principal a =', a)
func a = 30
Prog. principal a = 30
Se debe insistir en que se debe evitar a toda costa el uso de variables globales. Basta cambiar el identificador a por b en el programa principal del ejemplo anterior para que la salida del programa sea totalmente diferente.
¡Durante el curso queda terminantemente prohibido el uso de variables globales dentro de una función!
Funciones y tratamiento de excepciones#
Aviso
Este apartado requiere haber estudiado el tema Manejo de excepciones.
El tratamiento estructurado de excepciones y el enfoque EAFP (Easier to Ask Forgiveness than Permission), visto con anterioridad, alcanza su mayor utilidad cuando es aplicado conjuntamente con las funciones.
Veamos un ejemplo que implementa una función clónica del método index() de las listas.
# Función clónica del método index() de las listas
def indice(lista, valor):
for i, x in enumerate(lista):
if x == valor:
return i
raise ValueError(f'{valor} is not in list')
lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
try:
valor = 0
print(f'{valor} está en la posición {indice(lista, valor)} de la lista {lista}.')
except ValueError as error:
print(error)
# Usando el método index()
try:
valor = 0
print(f'{valor} está en la posición {lista.index(valor)} de la lista {lista}.')
except ValueError as error:
print(error)
0 is not in list
0 is not in list
La función indice() utiliza el mecanismo de excepciones para comunicar la existencia de un error que lanza una excepción ValueError, utilizando la sentencia raise. Esta excepción será manejada por el primer bloque try ... except que englobe la llamada a la función.
Nótese que una excepción termina inmediatamente el hilo de ejecución de la función.
Veamos otro ejemplo, en el que dividimos valor por valor dos listas. La idea es que, si un valor de una lista que actúa como denominador es nulo, entonces asignamos a su cociente el valor not a number nan.
# Función que divide valor por valor dos listas
def divide_dos_listas_entre_si(lista_num, lista_den):
lista_coc = []
for i in range(len(lista_num)):
try:
lista_coc.append(lista_num[i]/lista_den[i])
except ZeroDivisionError:
lista_coc.append(float('nan'))
return lista_coc
lista_num = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
lista_den_1 = [1]
lista_den_2 = [-5, 0, 'a', 4, 12, 21, 23, 34, 43, 123]
lista_den_3 = [-5, 0, 3, 4, 12, 21, 23, 34, 43, 123]
# Probamos dividir lista_num entre las tres listas siguientes, capturando las excepciones
try:
print(divide_dos_listas_entre_si(lista_num, lista_den_1))
except (IndexError, TypeError) as error:
print(error)
try:
print(divide_dos_listas_entre_si(lista_num, lista_den_2))
except (IndexError, TypeError) as error:
print(error)
try:
print(divide_dos_listas_entre_si(lista_num, lista_den_3))
except (IndexError, TypeError) as error:
print(error)
list index out of range
unsupported operand type(s) for /: 'int' and 'str'
[1.0, nan, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
En este ejemplo, podríamos haber optado por verificar de forma explícita las excepciones debidas a:
Las listas tienen tamaños diferentes
Datos incompatibles entre sí
Así, para manejar los tamaños diferentes, podríamos haber incluido dentro de la función lo siguiente:
if len(lista_num) != len(lista_den):
raise IndexError('Las listas tienen tamaños diferentes.')
Sin embargo, tal y como está programada la función, podemos ahorrárnoslo, pues el propio intérprete hará ese trabajo por nosotros.
Proceso de desarrollo de un programa#
Una vez conocido cómo definir funciones, tenemos muchas de las herramientas necesarias para acometer el desarrollo de un programa.
La programación es una tarea compleja a la que es mejor enfrentarse de manera iterativa.
Algunos pasos generales para hacerlo son:
Análisis del problema a resolver
Utilizar en esta etapa lápiz y papel y la ayuda de bosquejos, entre otros recursos.
Identificar los datos de entrada y cuáles deben ser las salidas buscadas, para todas las posibles condiciones.
Hacer cálculos paso a paso. Identificar resultados intermedios tratando de encontrar el algoritmo adecuado.
Versión inicial del problema
Una vez se llega a una primera solución en papel razonable, se pasa a programar, utilizando los recursos provistos por el lenguaje. Como se ha dicho, ya poseemos los elementos imprescindibles para resolver cualquier problema solucionable por un ordenador. Por supuesto, en la medida que avance el curso, los recursos a nuestra disposición crecerán.
Identificación de casos límite o especiales
Puede darse el caso de que el programa no funcione para los casos límites o especiales (¿funciona para el 2, que es el primer posible primo?, ¿pueden producirse divisiones por 0?, etc.). Es importante identificar esos casos para poder testarlos y, en su caso, corregir los fallos.
Casos de uso por parte del usuario
Por otro lado, es frecuente que en un primer esbozo del programa, se asuma que el usuario va a actuar de la forma prevista pero ¿qué pasa si no lo hace? (En el caso de los primos, ¿qué pasa si el número introducido es menor que dos o incluso negativo?). En ocasiones, el no prever todas estas posibles situaciones puede dar un resultado incorrecto o que el programa se interrumpa bruscamente por un error de ejecución. La solución de cada uno de los problemas detectados, implicará probablemente volver al paso 1 y la realización de modificaciones del código más o menos importantes, hasta que se llega a un código robusto y que funcione para todas las posibles entradas de datos. El manejo de excepciones tiene aquí un papel importante.
Legibilidad
Se debe tener en cuenta que un programa tiene otras virtudes además de dar las salidas correctas para todos los casos. Los programas deben ser legibles, estar escritos de forma clara y consistente, de manera que otros programadores o el mismo programador original pasado un tiempo, puedan comprenderlos con facilidad para hacer modificaciones o actualizaciones, que son frecuentemente necesarias en el ciclo de vida de un programa.
Los identificadores de las variables deben ser autoexplicativos, las estructuras de control deberán estar bien elegidas.
El sangrado del código y el uso correcto de los espacios en blanco ayuda notablemente en este aspecto. En este sentido, Python ha adoptado la decisión de exigir sintácticamente un sangrado correcto del código.
Refinamiento descendente
Frecuentemente ocurre que, en la medida en que el programa crece, se debe reestructurar el código. Buena legibilidad y facilidad de reestructuración están íntimamente ligadas. El refinamiento descendente agrupando código en funciones es la estrategia habitual.
Optimización del código
Las primeras versiones de un programa seguramente no constituyen la forma más eficiente (más rápida, por ejemplo) de resolver el problema. Un código que ya funciona correctamente puede estar sujeto a mejoras y optimizaciones. Aunque no se hará hincapié sobre este tema en un curso básico, en algunas ocasiones, sobre todo cuando se manipulan grandes volúmenes de datos, son importantes las consideraciones de cómo crece, por ejemplo, el tiempo de ejecución del programa cuando aumenta el tamaño de los datos de entrada. El encontrar un código eficiente es una tarea en general difícil, y debe ser en todo caso enfrentada cuando ya se tenga un programa básico que funcione correctamente.
Por otro lado, ¡no se debe caer en la trampa de la optimización prematura! En este sentido, es útil conocer que en la gran mayoría de los casos es bueno sacrificar la velocidad de ejecución en aras de una mayor claridad del código.
Documentación
Los comentarios en el código son útiles, pero es mejor evitarlos usando código autoexplicativo. Lo que sí es importante es documentar nuestros programas y, en especial, las funciones. Añadir en las zonas adecuadas del código información para explicar qué hacen y, en su caso, cómo lo hacen, y cómo deben ser utilizadas.
Introduciremos en breve el estándar de documentación Numpydoc.
Ejemplos de desarrollo de un programa sencillo#
Vamos a analizar a continuación algunos ejemplos, aplicando algunos de los pasos que acabamos de relatar.
El alumno atento observará que en muchos de los ejemplos que hemos visto o que veremos más adelante en temas sucesivos, no nos preocupamos de manejar las excepciones, por ejemplo, las causadas por entradas con un formato incorrecto de datos por parte del usuario. La razón principal es la de centrarnos en los aspectos clave de Python, evitando distracciones y exponiendo código de la forma más escueta posible. Esta táctica es la habitual en cualquier texto introductorio sobre lenguajes de programación.
Ejemplo 1: Determinación de si una serie de enteros son primos#
La última versión vista para determinar si un número es primo solo puede analizar un número cada vez. ¿Cómo modificarlo para darle la oportunidad al usuario de que analice sucesivamente varios enteros sin tener que ejecutar varias veces el programa?
La solución es utilizar otro bucle (bucles anidados), que incluya el código anterior, de manera que se pueda repetir cuantas veces se desee.
Comencemos por una versión ya vista en temas anteriores:
# Determina si un número entero es primo. (Versión 1)
numero = int(input('Deme un entero positivo mayor que 1: '))
es_primo = True # Variable centinela o bandera
for div in range(2, numero):
if numero % div == 0:
es_primo = False
break
if es_primo:
print(f'El número {numero} es primo.')
else:
print(f'El número {numero} no es primo.')
Vamos a estructurar el código usando refinamiento descendente usando una función es_primo(n).
# Determina si un número entero es primo, usando una función. (Versión 2)
def es_primo(n):
'''Si el número entero n es primo devuelve True. False en caso contrario.
La función es correcta para valores enteros mayores que 1'''
for div in range(2, numero):
if numero % div == 0:
return False
return True
numero = int(input('Deme un entero positivo mayor que 1: '))
if es_primo(numero):
print(f'El número {numero} es primo.')
else:
print(f'El número {numero} no es primo.')
Ahora, mediante un bucle, podemos conseguir que el programa solicite nuevos números hasta que el usuario desee finalizar.
# Determina si una serie de enteros son primos. Bucle infinito. (Versión 1)
while True:
numero = int(input('Deme un entero positivo mayor que 1: '))
if es_primo(numero):
print(f'El número {numero} es primo.')
else:
print(f'El número {numero} no es primo.')
opcion = input("Desea salir (s/n):")
if opcion == 's' or opcion == 'S':
break
La expresión de control del bucle while externo es la constante literal True: es un bucle infinito. Este tipo de bucles, muy habituales en programación, tienen asociada una sentencia break interna que permite su terminación prematura. Es el caso con el break de la estructura condicional donde se pregunta al usuario si quiere seguir introduciendo enteros.
Una alternativa al bucle infinito podría haber sido la siguiente:
# Determina si una serie de enteros son primos. Sin bucle infinito. (Versión 2)
opcion = 'n'
while opcion != 's':
numero = int(input('Deme un entero positivo mayor que 1: '))
if es_primo(numero):
print(f'El número {numero} es primo.')
else:
print(f'El número {numero} no es primo.')
opcion = input("Desea salir (s/n):").lower() # Convertimos a minúsculas
Ejemplo 1: Determinación de si una serie de enteros son primos con manejo de excepciones#
Aviso
Este apartado requiere haber estudiado el tema Manejo de excepciones.
En esta parte del desarrollo del programa ya podemos introducir los elementos que protegen al programa de entradas de datos incorrectas por parte del usuario, manejando las excepciones:
el usuario no introduce un valor entero
el valor entero introducido es inferior a
2
# Determina si una serie de enteros son primos. Con manejo de excepciones. (Versión 3)
while True:
try:
numero = int(input('Deme un entero positivo mayor que 1: '))
if numero < 2:
raise ValueError('El valor introducido debe ser mayor que 1.')
except ValueError as e:
print(e)
else:
if es_primo(numero):
print(f'El número {numero} es primo.')
else:
print(f'El número {numero} no es primo.')
finally:
opcion = input("Desea salir (s/n):").lower() # Convertimos a minúsculas
if opcion == 's':
break
Nótese que el manejo de excepciones se ha realizado de forma externa a la función es_primo().
Podríamos haber diseñado la función de tal forma que sea esta la que se preocupa de que el entero recibido sea válido.
# Función es_primo() con manejo interno de excepciones
def es_primo_con_excepciones(n):
'''Si el número entero n es primo devuelve True. False en caso contrario.
Si el valor n no es entero o es menor que 1 lanza una excepción ValueError'''
if type(n) != int:
raise TypeError(f'El parámetro de entrada {n} no es de tipo int.')
elif n < 2:
raise ValueError('El valor introducido debe ser mayor que 1.')
for div in range(2, n):
if n % div == 0:
return False
return True
try:
valor = 3.4
if es_primo_con_excepciones(valor):
print(f'{valor} es primo.')
except (ValueError, TypeError) as error:
print(error)
try:
valor = -1
if es_primo_con_excepciones(valor):
print(f'{valor} es primo.')
except (ValueError, TypeError) as error:
print(error)
try:
valor = 97
if es_primo_con_excepciones(valor):
print(f'{valor} es primo.')
except (ValueError, TypeError) as error:
print(error)
El parámetro de entrada 3.4 no es de tipo int.
El valor introducido debe ser mayor que 1.
97 es primo.
El criterio para manejar o detectar las excepciones dentro de una función no es una ciencia exacta. Verificar la validez de los datos de entrada o de algún resultado intermedio es una tarea que consume tiempo de computación. Y en determinadas aplicaciones puede que sea más práctico dejar esa responsabilidad al programador usuario de la función y que sea éste el que garantice su correcto uso. Es lo que hicimos en la versión previa a esta última.
Esto pone de relevancia lo importante que es la documentación de las funciones. Entre otras cosas, la documentación debe informar de aquellas situaciones que eventualmente puedan generar excepciones, si estas son manejadas (try) o si son levantadas (raise).
La versión 3 del programa hace lo que nos proponíamos, aunque su uso por el usuario puede ser algo engorroso debido a la pregunta explícita sobre si se desea salir o no del programa.
En ocasiones, la naturaleza del problema es tal que el rango posible de la entrada de datos está limitado. Este hecho se puede utilizar en nuestra ventaja para simplificar el diseño del programa y mejorar la experiencia del usuario. ¿Cómo se hace? Simplemente se utilizan los valores no útiles del rango de entrada para señalar otros caminos al programa.
En el caso que nos ocupa se puede hacer, por ejemplo, que la introducción por parte del usuario de un valor menor que 2 señale su deseo de abandonar el programa. En caso contrario, se continuaría con las iteraciones en el bucle externo, preguntando por otros enteros a considerar.
Por tanto, la introducción de un valor menor que 2 deja de ser una excepción. Es parte de los valores válidos que puede utilizar el usuario.
# Determina si una serie de enteros son primos (versión 4)
numero = 2 # Valor inicial arbitrario para que entre al bucle la primera vez
while numero > 1:
print('\nPara salir introduzca un entero menor que 2.')
try:
numero = int(input('Deme un entero: '))
except ValueError as e:
print(e)
else:
if numero > 1:
if es_primo(numero):
print(f'El número {numero} es primo.')
else:
print(f'El número {numero} no es primo.')
print("Fin del programa.")
Ejemplo 2: Determinación del número \(\pi\) mediante la serie de Euler#
La constante \(\pi\) es una de la más importantes en matemáticas. Conocemos que se trata de un número real con infinitas cifras no periódicas tanto en su representación decimal como en cualquier otra base numérica.
En el módulo math se tiene una aproximación bastante precisa del mismo, suficiente para las aplicaciones ingenieriles concebibles.
En el siguiente ejemplo se va a proceder a su estimación, utilizando uno de las tantas series que se demuestra que convergen a dicho número.
En particular, se tiene la siguiente serie infinita definida para todos los enteros positivos \(k\):
Nótese que la solución de este problema, la suma en principio ilimitada de un conjunto de números, no se puede emprender sin la presencia de un bucle.
Conviene, antes de comenzar, analizar en detalle el mecanismo propuesto para la generación de una aproximación de \(\pi\):
¿Sabríamos antes de entrar al bucle el número de iteraciones a ejecutar? Únicamente lo sabríamos si alguien nos dijera que quiere hacer una aproximación que involucre \(n\) términos. Esto haría decantarnos hacia la utilización de un bucle
for.Sin embargo, lo razonable es plantear el problema de forma que el resultado se aproxime a \(\pi\) por debajo de una tolerancia o cuando se cumpla una condición de terminación previamente elegida por el usuario. Esto hace que nos decantemos por utilizar un bucle
while.El trabajo con bucles frecuentemente requiere:
Inicializar variables antes de entrar al bucle.
Identificar qué es lo que variará de una iteración a otra y qué objetivos parciales se van cumpliendo de forma tal que en cada iteración nos vayamos acercando cada vez más a la solución buscada.
Establecer la condición lógica que determine la permanencia en el bucle.
Finalmente, comprobar que el bucle funcione también para los casos límite.
# Determinación del número pi mediante la serie de Euler (Versión 1)
tolerancia = 1e-6
suma_parcial = 0.0
termino = tolerancia + 1 # Para obligar a entrar en el bucle
k = 0
while abs(termino) > tolerancia:
k += 1
termino = (-1)**(k + 1)/k**2
suma_parcial += termino
pi_aprox = (12.0*suma_parcial)**0.5
print(f'La aproximación de PI hallada es {pi_aprox} y se obtuvo en {k} iteraciones.')
La aproximación de PI hallada es 3.141591699614916 y se obtuvo en 1000 iteraciones.
En el ejemplo anterior se requiere un contador,
k, que recorra los enteros que participan en la definición de cada término de la serie y que debe ser incrementado en cada iteración.También de una variable tipo acumulador,
suma_parcial, que siempre va a contener la suma de todos los términos que se hayan calculado hasta la iteración de que se trate.Observe el uso de de la asignación compuesta
+=para actualizar tanto el acumulador como el contador.Se define por comodidad una variable,
termino, que contiene el valor del término que se añade a la serie en cada iteración. Se hace esto porque se ha decidido utilizar como criterio de permanencia en el bucle el hecho de que el aporte nuevo a la estimación del valor desuma_parcialsea (en valor absoluto) mayor que un valor elegido positivo pequeño,tolerancia(en este caso una millonésima:1e-6).Vea que el uso de la función nativa
abs()en la expresión de control delwhilees indispensable, puesto que el valor de los términos nuevos van cambiando de signo de una iteración a la siguiente.Antes de entrar al bucle, se eligen los valores iniciales para el contador y el acumulador. En el caso del contador se inicializa a
0. El acumulador se inicializa a0.0.A la variable
termino, que participa en la expresión de control del bucle, se le da un valor inicial arbitrario, en este casotolerancia + 1. El objetivo aquí es darle un valor que sea mayor quetoleranciay que fuerce, por tanto, la primera entrada al bucle.
El orden en que aparecen las sentencias dentro del bucle es importante (aunque no es la única posible si el problema se replanteara de otra forma). Es conveniente realizar algunas iteraciones manuales para ver que el esquema elegido funciona correctamente.
Al salir del bucle se saca por pantalla tanto la aproximación hallada como el número de iteraciones que tomó el calcularla.
Pruebe a cambiar el valor de la tolerancia. En cualquier caso, se debe recordar que la precisión con la que son manipulados los float en Python es limitada.
Vamos a estructurar el código, encapsulando la serie dentro de una función calcula_pi_euler(tol=1e-6). Nótese el valor de la tolerancia por defecto.
Dado que el numerador es alternadamente 1 y -1 se ha hecho una pequeña optimización sustituyendo el cálculo del numerador (-1)**(k + 1).
# Determinación del número pi mediante la serie de Euler, usando una función (Versión 2)
def calcula_pi_euler(tol=1e-6):
'''Calcula el número pi mediante la serie de Euler.
El valor tol determina la precisión. Cuando abs(termino) <= tol
se da por finalizado el cálculo.'''
suma_parcial = 0.0
termino = tol + 1 # Para obligar a entrar en el bucle
k = 0
num = 1
while abs(termino) > tol:
k += 1
termino = num/k**2
suma_parcial += termino
num = -num
return (12.0*suma_parcial)**0.5
pi_aprox = calcula_pi_euler(1.e-7)
print(f'La aproximación de PI hallada es {pi_aprox}')
La aproximación de PI hallada es 3.1415927490089612
Nótese que, si el usuario utiliza una tolerancia cercana a 0 o negativa como argumento, el bucle será de facto un bucle infinito. Dejamos al alumno que haya estudiado manejo de excepciones que modifique la función anterior levantando una excepción cuando el parámetro de entrada tol sea incorrecto.
El alumno no debe perder de vista aspectos relativos a la precisión con sumatorios con muchos términos y con expresiones tales como:
Conforme el valor \(k\) aumenta, la representación finita de los datos float entra en juego, por lo que el error cometido al calcular cada término hará inservible el utilizar una tolerancia excesivamente pequeña.
Respecto a los errores acumulados en series de muchos términos, el siguiente sencillo ejemplo ilustra este problema:
incr = 0.1 # La representación no es exacta
suma = 0
for i in range(10**6):
suma += incr
print(f'El valor esperado es {10**6} frente al obtenido {suma}')
El valor esperado es 1000000 frente al obtenido 100000.00000133288
Ejemplo 3: Algoritmo para la determinación del máximo común divisor (MCD)#
Se trata de encontrar el mayor número que divida exactamente dos números enteros positivos dados. El algoritmo que resuelve el problema es uno de los más antiguos y famosos y se atribuye a Euclides.
Sean dos enteros positivos: \(p\) y \(q\) (suponiendo \(p >= q\)). En general, se puede plantear que \(p=q*c+r\), donde \(c\) y \(r\) son el cociente y resto respectivamente.
Es posible demostrar que el máximo común divisor de \(p\) y \(q\) es el mismo que el de \(q\) y \(r\). Sea \(mcd\) el máximo común divisor de \(p\) y \(q\). Como \(p=q*c+r\) y \(mcd\) divide a \(p\) y \(q\) también divide a \(q\) y \(r\). Si existiera otro número mayor que \(mcd\) que divide a \(q\) y \(r\), también dividiría a \(p\), lo que contradiría que \(mcd\) es un máximo común divisor.
Este mismo razonamiento puede repetirse cuantas veces se quiera, haciendo que el dividendo sea el anterior divisor y el nuevo divisor el antiguo resto, hasta que eventualmente, con toda seguridad, se obtendrá un resto igual a cero (puesto que los sucesivos restos van inevitablemente descendiendo y deben ser positivos). Cuando el resto es cero, el último divisor que se utilizó es precisamente el MCD.
Si el divisor inicial es \(0\), el MCD es el dividendo y si ambos son ceros el MCD es \(0\).
Una primera versión del algoritmo de Euclides podría ser la siguiente:
# Halla el MCD de dos números enteros naturales, incluido el 0 (Versión 1)
# ENTRADA DE DATOS
print('Introduzca dos enteros, para los que se calculará el MCD.')
while True:
dividendo = int(input('Introduzca el primer número (>=0): '))
divisor = int(input('Introduzca el segundo número (>=0): '))
if dividendo < 0 or divisor < 0:
print("Ambos números deben ser iguales o mayores que 0.\n")
else:
break
# ALGORITMO MCD
if dividendo < divisor: # Asegurando que el dividendo sea mayor que el divisor
dividendo, divisor = divisor, dividendo
if dividendo == divisor == 0:
mcd = 0
elif divisor == 0:
mcd = dividendo
else:
dividendo_copia = dividendo
divisor_copia = divisor
resto = dividendo % divisor # Hallamos el primero resto fuera del bucle
while resto != 0:
dividendo = divisor
divisor = resto
resto = dividendo % divisor
mcd = divisor
# SALIDA
print(f'El MCD de {dividendo_copia} y {divisor_copia} es {mcd}.')
Una posible ejecución del programa sería:
Introduzca dos enteros, para los que se calculará el MCD.
Introduzca el primer número (>=0): 11025
Introduzca el segundo número (>=0): 6615
El MCD de 11025 y 6615 es 2205.
Podemos ver claramente las tres partes típicas de un programa:
Entrada de datos
Algoritmo
Salida de datos
Centrándonos en el algoritmo, nótese que:
la condición de permanencia en el bucle es que el resto sea diferente de cero.
antes de entrar al bucle se hace una primera división para obtener un resto válido.
dentro del bucle la tarea es entonces acomodar lo que antes era el divisor de forma que se convierta en el nuevo dividendo y que el antiguo resto pase a ser el divisor. El orden de estas asignaciones es crucial.
la última sentencia del bucle halla el nuevo resto que será considerado en la siguiente evaluación del control del bucle.
al salir del bucle el MCD es el valor que está en la variable
divisor.para la salida ha sido necesario guardar una copia de los valores originales de
dividendoydivisor.
Debido al carácter iterativo de un bucle, es primordial elegir el momento clave en que se realiza la división entera y que las variables que participan hayan sido actualizadas de forma que desempeñen el rol adecuado en la iteración de que se trate. Esto implica, en muchas ocasiones, hacer reasignaciones como se muestra en el ejemplo.
Es importante antes de entrar al bucle, garantizar que el dividendo es mayor o igual que el divisor. Esto se hace mediante el correspondiente if. Véase que el intercambio entre los contenidos de dividendo y divisor se hace en una sola línea, aprovechando la facilidad que brinda Python y que no existe en muchos otros lenguajes. ¿Se podría hacer uso de esta asignación doble dentro del bucle? ¿Cómo se haría?
En la siguiente versión, vamos a encapsular la entrada de datos en una función pide_valores() y el algoritmo de Euclides en una función mcd_euclides(n, m).
# Halla el MCD de dos numeros enteros naturales, incluido el 0, usando funciones (Versión 2)
def pide_valores():
'''Solicita dos valores enteros exigiendo que sean >= que 0'''
print('Introduzca dos enteros, para los que se calculará el MCD.')
while True:
num1 = int(input('Introduzca el primer número (>=0): '))
num2 = int(input('Introduzca el segundo número (>=0): '))
if num1 < 0 or num2 < 0:
print("Ambos números deben ser iguales o mayores que 0.\n")
else:
break
return num1, num2
def mcd_euclides(dividendo, divisor):
'''Calcula es Máximo Común Divisor de los valores de entrada.
Para el correcto funcionamiento los dos valores deben ser enteros y >= que 0.
El orden relativo es indiferente.'''
if dividendo < divisor:
dividendo, divisor = divisor, dividendo
if dividendo == divisor == 0:
mcd = 0
elif divisor == 0:
mcd = dividendo
else:
resto = dividendo % divisor
while resto != 0:
dividendo, divisor = divisor, resto
resto = dividendo % divisor
mcd = divisor
return mcd
num1, num2 = pide_valores()
print(f'El MCD de {num1} y {num2} es {mcd_euclides(num1, num2)}.')
Véase como el uso de funciones y su poder de abstracción ha reducido el programa principal al uso de ¡dos sentencias!
Ejemplo 3: Algoritmo para la determinación del máximo común divisor (MCD) con manejo de excepciones#
Aviso
Este apartado requiere haber estudiado el tema Manejo de excepciones.
Veamos una versión de la función pide_valores() más robusta manejando excepciones.
# Versión manejando excepciones
def pide_valores():
'''Solicita dos valores enteros exigiendo que sean >= que 0'''
print('Introduzca dos enteros, para los que se calculará el MCD.')
while True:
try:
num1 = int(input('Introduzca el primer número (>=0): '))
num2 = int(input('Introduzca el segundo número (>=0): '))
if num1 < 0 or num2 < 0:
raise ValueError('Ambos números deben ser iguales o mayores que 0.')
except ValueError as error:
print(error)
else:
break
return num1, num2
Nótese que esta versión maneja un posible error en el formato de la entrada de datos sin que el programa finalice bruscamente.
En este caso, consideramos que la documentación de la función mcd_euclides() ya advierte de que debe usarse con enteros positivos o nulos. Es responsabilidad del usuario garantizar esa restricción. Por ello, no hemos añadido manejo de excepciones. De hecho, es lo que hacemos en la función pide_valores() como paso previo a utilizar mcd_euclides().
Ejemplo 4: Conjetura de Collatz#
La conjetura de Collatz propone que, para cualquier número positivo, tras el proceso iterativo:
se alcanza en algún momento para \(n\) la unidad.
Este hecho no está demostrado, de ahí que se trate de una conjetura. El siguiente código implementa el algoritmo propuesto, pero añade un contador para acotar el número máximo de iteraciones.
# Conjetura de Collatz (Versión 1)
# ENTRADA DE DATOS
n = 0
while n < 1:
n = int(input("Dame un número entero positivo: "))
if n < 1:
print("¡ERROR!. El número debe ser positivo.")
num_max_iteraciones = 1e10
# ALGORITMO
iteraciones = 0
while n != 1 and iteraciones < num_max_iteraciones:
if n % 2 == 0: # Par
n = n // 2
else:
n = 3*n + 1
iteraciones += 1
# SALIDA
if n == 1:
print(f'Se ha llegado a 1 en {iteraciones} iteraciones.')
else:
print(f'No se ha llegado a 1 en {iteraciones} iteraciones. ¡Se debe investigar más!')
Una posible ejecución del programa sería:
Dame un número entero positivo: 347373673
Se ha llegado a 1 en 269 iteraciones.
Fuera del bucle se solicita el valor inicial de \(n\) y se inicializa el contador. Dentro del bucle, simplemente se actualiza el valor de \(n\) según el procedimiento dado. Se saldrá del bucle cuando \(n\) llega al valor de \(1\) (reforzando nuestra convicción de que la conjetura de Collatz es válida) o cuando el contador llega al valor determinado por el límite de iteraciones.
De forma similar al ejemplo anterior, vamos a utilizar funciones para mejorar el programa.
# Conjetura de Collatz con funciones (Versión 2)
def pide_valor(inf=0):
'''Solicita un valor entero exigiendo que sea >= que el parámetro de entrada inf'''
while True:
num = int(input(f'Introduzca un entero (>={inf}): '))
if num < inf:
print('El número debe ser positivo.')
else:
break
return num
def collatz(n, max_iter=1e10):
'''Implementa la conjetura de Collatz con un valor límite de iteraciones max_iter.
Devuelve True o False en función de si se cumple la conjetura para el valor de entrada num
y el número de iteraciones que se han necesitado.
El valor introducido debe ser un entero positivo.'''
iteraciones = 0
while n != 1 and iteraciones < max_iter:
if n % 2 == 0:
n = n // 2
else:
n = 3*n + 1
iteraciones += 1
if n == 1:
return True, iteraciones
else:
return False, iteraciones
n = pide_valor(1)
resultado = collatz(n, 1000)
if resultado[0]:
print(f'Desde el valor {n}, se ha llegado a 1 en {resultado[1]} iteraciones.')
else:
print(f'Desde el valor {n}, no se ha llegado a 1 en {resultado[1]} iteraciones. ¡Se debe investigar más!')
En esta variante, la función pedir_valor(inf=0) incorpora como argumento un límite inferior para que el valor introducido desde teclado sea válido. Por defecto, el valor 0.
El resultado de la función collatz() es una tupla, formada por una boolena que determina si la conjetura se cumplió y el número de iteraciones.
Los valores intermedios por los que pasa \(n\) hasta finalmente llegar a \(1\) oscilan con amplitudes muy grandes.
Aprovechando esta característica, vamos a introducir otra idea básica, que al igual que los acumuladores, permite obtener alguna característica del conjunto de números procesados mediante un bucle.
Se trata de obtener, el valor máximo o mínimo de todos los valores procesados. En el caso que nos ocupa, sería interesante obtener al final cuál ha sido el valor mayor por el que ha pasado \(n\).
La idea para resolver este tipo de problema es tan sencilla como efectiva y se puede enunciar de la siguiente forma para el caso de querer obtener el valor máximo:
Fuera del bucle, inicializar una variable,
maximo, con el primer valor del conjunto de números (o con el menor de los valores del rango esperado, si es que esta información se conoce)Si el algoritmo encuentra un \(n\) impar, interrogar mediante un condicional, si el valor actualmente inspeccionado del conjunto de números es mayor que el que teníamos memorizado en
maximoy, en caso afirmativo, actualizar el valor de esta última variable. Nótese que, si \(n\) es par, el nuevo valor \(n\) será necesariamente inferior.
Basta añadir a la función collatz() un nuevo componente en la tupla resultado de salida.
def collatz(n, max_iter=1e10):
'''Implementa la conjetura de Collatz con un valor límite de iteraciones max_iter.
Devuelve True o False en función de si se cumple la conjetura para el valor de entrada num,
el número de iteraciones que se han necesitado y el máximo valor alcanzado'''
iteraciones = 0
maximo = n # inicializamos a un valor conocido
while n != 1 and iteraciones < max_iter:
if n % 2 == 0:
n = n // 2
else:
n = 3*n + 1
if n > maximo:
maximo = n
iteraciones += 1
if n == 1:
return True, iteraciones, maximo
else:
return False, iteraciones, maximo
Ejemplo 5: Algoritmo de ordenación por inserción#
Una de las tareas más habituales en programación es la de ordenar una colección de datos. Es tan común que existen funciones y métodos ya listos para ser utilizados, predefinidos en el lenguaje, como por ejemplo, la función nativa sorted() o el método .sort() de las listas.
La razón que justifica la importancia de tener listas ordenadas radica en la facilidad posterior para encontrar elementos, al poder realizar sobre ellas las llamadas búsquedas binarias, mucho más eficientes que una búsqueda secuencial.
Existen muchos algoritmos de ordenación, de diferente grado de complejidad y eficiencia. El algoritmo de ordenación por inserción o método de la baraja es bastante simple y resulta eficaz para colecciones no muy grandes.
Supongamos que se quiere ordenar una lista dada de menor a mayor. La idea básica consiste en dividir (conceptualmente) la lista en dos:
una primera sublista que se mantiene siempre ordenada
una sublista con los elementos restantes, que están en principio desordenados
De forma iterada, se extrae el primer elemento de la sublista desordenada y se inserta en el lugar adecuado en la sublista ordenada. De esta forma, en cada iteración la sublista ordenada crece en un elemento y la desordenada disminuirá en uno.
¿Cómo inicializar el algoritmo? El tamaño inicial de la sublista ordenada será uno y el elemento que la compone será el primer elemento de la lista original ¡que está, por supuesto, ordenado! El resto de elementos constituyen la lista inicial desordenada.
# Ordenación por inserción (Versión 1)
enteros = [20, 1, 4, -1, -10, 0, 1, 6]
for i in range(1, len(enteros)): # Recorre la sublista desordenada
j = i
tmp = enteros[i] # Copia temporal del nuevo elemento
# Bucle que deja un hueco para insertar el nuevo elemento en la sublista ordenada
while j > 0 and enteros[j-1] > tmp:
enteros[j] = enteros[j-1]
j -= 1
enteros[j] = tmp # Inserta el nuevo elemento
print(enteros)
[-10, -1, 0, 1, 1, 4, 6, 20]
Es importante entender que el algoritmo anterior ordena la lista in situ. Consta de dos bucles anidados:
El
forexterno recorre todos los elementos a partir del segundo, utilizando el índicei, esto es, recorre uno por uno todos los elementos de la sublista desordenada.El bucle interno, por su parte, utiliza un
whiley otro índicejpara recorrer la sublista de los elementos ya ordenados, hasta encontrar el sitio que le corresponde al elemento que debe ser insertado y que está provisionalmente almacenado entmp. Nótese que mientras no se encuentra la posición adecuada en la sublista ordenada, los elementos de la misma son recolocados apropiadamente ascendiéndolos una posición.
¿Cómo modificarías el código previo para que se ordene de mayor a menor?
Vamos ahora a encapsular el algoritmo en una función sort_insercion(lista, reverse=False). Si el parámetro reverse es True, se ordenará de mayor a menor.
# Ordenación por inserción, usando funciones (Versión 2)
def compara(x, y, reverse):
'''Compara dos valores en función del parámetro reverse'''
if reverse:
return x < y
else:
return x > y
def sort_insercion(lista, reverse=False):
'''Ordena una lista de menor a mayor si reverse es False.
De mayor a menor si reverse es True'''
for i in range(1, len(lista)):
j = i
tmp = lista[i]
while j > 0 and compara(lista[j-1], tmp, reverse):
lista[j] = lista[j-1]
j -= 1
lista[j] = tmp
enteros = [20, 1, 4, -1, -10, 0, 1, 6]
sort_insercion(enteros, True)
print(enteros)
[20, 6, 4, 1, 1, 0, -1, -10]
Nótese que la lista enteros, externa a la función, ha sido modificada dentro de la función. No es una función pura: es la consecuencia del carácter mutable de las listas.
Ejemplo 6: La búsqueda binaria#
La búsqueda binaria es un método de búsqueda extraordinariamente eficiente cuando el ítem buscado pertenece a una secuencia ordenada. También se conoce al algoritmo como búsqueda por bisección o búsqueda dicotómica.
La idea es en cada iteración dividir el espacio de búsqueda entre dos, tomando el valor intermedio de la secuencia. Esta subdivisión entre dos es la que da nombre al algoritmo.
Comparando el valor buscado con el valor situado en la posición intermedia de la secuencia, tenemos 3 opciones:
El valor intermedio coincide con el buscado, con lo que el objetivo está conseguido.
El valor intermedio es inferior, con lo que, de encontrarse en la secuencia el valor buscado, al estar ordenada, debemos seguir intentándolo en la subsecuencia de valores superiores al intermedio.
El valor intermedio es superior, con lo que, de forma análoga al punto 2, debemos seguir buscándolo en la subsecuencia de valores inferiores al intermedio.
Para ver paso a paso el desempeño del algoritmo, vamos utilizar un ejemplo con una lista ordenada de números enteros.
lista = [-5, 2, 3, 4, 12, 21, 23, 34, 43, 123]
Para controlar la sublista con la que vamos a trabajar de forma iterada, vamos a manejar dos valores, dos punteros, que nos indican los índices inferior y superior de la sublista.
Inicialmente, nuestra sublista es la lista original. Por tanto, tendríamos:
inf = 0
sup = len(lista) - 1
Imaginemos que el valor a buscar es el 0. Veamos la evolución del algoritmo paso a paso sin usar bucles y actualizando los punteros inf y sup de forma manual. Probemos el valor situado en la posición intermedia de la lista original.
def obtiene_nuevos_limites(lista, valor, inf, sup):
'''Devuelve los nuevos límites de búsqueda de valor en la lista'''
mitad = (inf+sup)//2 # División entera, pues los índices son enteros
print(f'Probamos con la posición {mitad}.')
if valor_buscado < lista[mitad]:
print(f'El valor {valor_buscado} se encontraría en la sublista inferior de índices [{inf},{mitad-1}].')
return inf, mitad-1
elif valor_buscado > lista[mitad]:
print(f'El valor {valor_buscado} se encontraría en la sublista superior de índices [{mitad+1},{sup}].')
return mitad+1, sup
else:
print(f'El valor {valor_buscado} se encuentra en la posición {mitad}.')
return mitad, mitad
valor_buscado = 0
inf = 0
sup = len(lista) - 1
inf, sup = obtiene_nuevos_limites(lista, valor_buscado, inf, sup)
Probamos con la posición 4.
El valor 0 se encontraría en la sublista inferior de índices [0,3].
Dado que el índice mitad inicialmente vale 4 y lista[4] es 12, de encontrarse en la lista inicial, el valor buscado 0 deberá estar en la sublista comprendida entre los valores inf y mitad-1, es decir, en la sublista comprendida entre los índices 0 y 3.
Repitamos el proceso con una celda similar a la anterior, con los valores inf y sup actualizados.
inf, sup = obtiene_nuevos_limites(lista, valor_buscado, inf, sup)
Probamos con la posición 1.
El valor 0 se encontraría en la sublista inferior de índices [0,0].
Ahora el índice mitad vale 1 y lista[1] es 2. Al igual que antes, de encontrarse en la lista inicial, el valor buscado 0 deberá estar en la sublista comprendida entre los valores inf y mitad-1, es decir, en la sublista comprendida entre los índices 0 y 0. Nótese que esta sublista tiene ya un único elemento. ¡Se nos acaban las oportunidades!
Repitamos el proceso con una celda similar a la anterior, con los valores inf y sup actualizados.
inf, sup = obtiene_nuevos_limites(lista, valor_buscado, inf, sup)
Probamos con la posición 0.
El valor 0 se encontraría en la sublista superior de índices [1,0].
Obviamente el valor 0 no se encuentra en la sublista y, además, nuestro proceso nos arroja un resultado absurdo: el valor buscado debe estar en la sublista situada entre las posiciones [1,0]. Es absurdo puesto que lógicamente debe cumplirse inf <= sup.
Esta situación es la prueba de que el valor buscado no se encuentra en la lista. Además, nos da la clave para transformar nuestro proceso secuencial en un proceso iterativo.
Veámoslo ya todo integrado en el siguiente fragmento de código:
# Búsqueda binaria. (Versión 1)
lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
inf = 0
sup = len(lista) - 1
valor = int(input('Introduzca un valor entero: '))
encontrado = False # Centinela
while inf <= sup and not encontrado:
mitad = (inf+sup)//2
if valor < lista[mitad]:
sup = mitad - 1
elif valor > lista[mitad]:
inf = mitad + 1
else:
encontrado = True
if encontrado:
print(f'El valor {valor} se encuentra en la posición {mitad}.')
else:
print(f'El valor {valor} no se encuentra en la lista.')
Un ejemplo de ejecución es el siguiente:
Introduzca un valor entero: 23
El valor 23 se encuentra en la posición 6.
La búsqueda binaria necesita en el peor de los casos un tiempo logarítmico de operaciones, \(O(\log n)\) comparaciones, donde \(n\) es el número de elementos de la lista. Así, para una lista con \(2^n\) ítems se necesitarán a lo sumo \(n\) comprobaciones.
Lo lógico es que este algoritmo de búsqueda binaria lo encapsulemos en una función, busqueda_binaria(lista, valor), para su fácil reutilización. Esta función devolverá la posición en la que se encuentra el elemento. La cuestión que nos podemos plantear es: ¿qué devolvemos si el valor buscado no se encuentra en la lista?
En la bibliografía aparecen diferentes posibilidades:
Devolver un valor negativo, típicamente -1. Dado que un valor negativo no puede ser un índice válido de una lista es una forma de indicarle al usuario de la función que no se ha encontrado el valor.
Devolver la palabra reservada
None, que es una forma de indicar que no se ha encontrado el valor.Levantar una excepción
ValueError. Es la estrategia más pitónica. De hecho, como ya hemos visto, es la que adopta Python con el métodoindex()de las listas, donde la única diferencia con la búsqueda binaria es que no se presupone que la lista esté previamente ordenada. El mensaje que lanza Python en este método asociado a la excepción es:x is not in list, dondexes el valor buscado.
Veamos la segunda opción.
# Búsqueda binaria, con funciones devolviendo None en caso de no tener éxito (Versión 2)
def busqueda_binaria(lista, valor):
'''
Devuelve la posición de valor en una lista ordenada.
El funcionamiento será incorrecto si la lista no está ordenada.
Parameters
----------
lista : list
Lista ordenada de valores para los que están definidos los operadores ==, < y >.
valor : type
Cualquier valor del mismo tipo o compatible con los de la lista.
Returns
-------
indice : int o None
Índice de la lista en la que se ha encontrado el valor o None si no se encuentra.
Example
-------
>>> lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
>>> print(busqueda_binaria(lista, 3))
2
'''
inf = 0
sup = len(lista) - 1
while inf <= sup:
indice = (inf+sup)//2
if valor < lista[indice]:
sup = indice - 1
elif valor > lista[indice]:
inf = indice + 1
else:
return indice # Nos ahorramos la booleana encontrado
# Si llegamos aquí es que el valor no se encuentra en la lista
return None
lista = ['adiós', 'buenos días', 'hasta luego', 'hola', 'suerte']
valor = 'hola'
indice = busqueda_binaria(lista, valor)
if indice is not None:
print(f'{valor} está en la posición {indice} de la lista {lista}.')
else:
print(f'{valor} no está en la lista {lista}')
lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
valor = 0
indice = busqueda_binaria(lista, valor)
if indice is not None:
print(f'{valor} está en la posición {indice} de la lista {lista}.')
else:
print(f'{valor} no está en la lista {lista}')
hola está en la posición 3 de la lista ['adiós', 'buenos días', 'hasta luego', 'hola', 'suerte'].
0 no está en la lista [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
En la anterior celda vemos la función documentada y unas líneas que nos muestran un ejemplo de uso. La función nativa help(), cuando es llamada con el nombre de una función, imprime en la consola o ventana esta información.
help(busqueda_binaria)
Help on function busqueda_binaria in module __main__:
busqueda_binaria(lista, valor)
Devuelve la posición de valor en una lista ordenada.
El funcionamiento será incorrecto si la lista no está ordenada.
Parameters
----------
lista : list
Lista ordenada de valores para los que están definidos los operadores ==, < y >.
valor : type
Cualquier valor del mismo tipo o compatible con los de la lista.
Returns
-------
indice : int o None
Índice de la lista en la que se ha encontrado el valor o None si no se encuentra.
Example
-------
>>> lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
>>> print(busqueda_binaria(lista, 3))
2
Ejemplo 6: La búsqueda binaria con manejo de excepciones#
Aviso
Este apartado requiere haber estudiado el tema Manejo de excepciones.
# Búsqueda binaria, con funciones y manejo de excepciones (Versión 3)
def busqueda_binaria(lista, valor):
'''
Devuelve la posición de valor en una lista ordenada.
El funcionamiento será incorrecto si la lista no está ordenada.
Parameters
----------
lista : list
Lista ordenada de valores para los que están definidos los operadores ==, < y >.
valor : type
Cualquier valor del mismo tipo o compatible con los de la lista.
Returns
-------
indice : int
Índice de la lista en la que se ha encontrado el valor.
Raises
------
ValueError
Si el valor no se encuentra en la lista.
Example
-------
>>> lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
>>> print(busqueda_binaria(lista, 3))
2
'''
inf = 0
sup = len(lista) - 1
while inf <= sup:
indice = (inf+sup)//2
if valor < lista[indice]:
sup = indice - 1
elif valor > lista[indice]:
inf = indice + 1
else:
return indice # Nos ahorramos la booleana encontrado
# Si llegamos aquí es que el valor no se encuentra en la lista
raise ValueError(f'{valor} no está en la lista')
lista = ['adiós', 'buenos días', 'hasta luego', 'hola', 'suerte']
try:
valor = 'hola'
print(f'{valor} está en la posición {busqueda_binaria(lista, valor)} de la lista {lista}.')
except ValueError as error:
print(error)
lista = [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
try:
valor = 0
print(f'{valor} está en la posición {busqueda_binaria(lista, valor)} de la lista {lista}.')
except ValueError as error:
print(error, lista)
hola está en la posición 3 de la lista ['adiós', 'buenos días', 'hasta luego', 'hola', 'suerte'].
0 no está en la lista [-5, 1, 3, 4, 12, 21, 23, 34, 43, 123]
Testar nuestro código y, en particular, las funciones, es fundamental antes de incorporarlo a otras partes de nuestros programas. ¡Acostúmbrate a comprobar por partes tu código! En breve, veremos cómo hacerlo de forma algo más sistemática.
