Módulo random#
Generador de números aleatorios
Distribuciones uniformes
Distribución normal
Ejemplos de aplicación
Generador de números aleatorios#
Un generador de números aleatorios (random number generator) es un programa que genera una secuencia aleatoria, en principio, de forma impredecible.
Su uso es fundamental en aplicaciones de juegos de ordenador, plataformas de apuestas en línea, criptografía y en otras muchas aplicaciones de orden científico para simular o tomar decisiones de forma aleatoria.
En realidad, la mayor parte de los generadores de números aleatorios son, en realidad, pseudoaleatorios: a partir de un valor inicial, la semilla (seed), generan una secuencia \(\{rnd1, rnd2, rnd3, ...\}\) que es ¡siempre la misma!
La semilla#
Variando la semilla podemos hacer que la secuencia cambie de una ejecución a otra de nuestro programa. De hecho, los generadores aleatorios sofisticados permiten inicializar la semilla de forma cuidadosa porque, no en vano, debemos evitar que un posible intruso (hacker), analizando varios elementos de la secuencia, adivine la semilla inicial y sea capaz de reproducir, es decir, predecir, los siguientes valores generados. Esto sería inadmisible en una aplicación web de póquer o de cifrado de mensajes, por ejemplo.
Sin embargo, poder usar repetidamente la misma semilla es también una característica deseable, ya que permite reproducir cuantas veces sea necesario el mismo experimento y, por ejemplo, depurar un posible error detectado.
Generador de aleatorios en Python#
El módulo Random de Python usa por defecto el generador de pseudoaleatorios Mersenne Twister, uno de los más utilizados en diferentes lenguajes de programación para aplicaciones científicas. Sin embargo, es totalmente inapropiado para una aplicación de tipo criptográfico. En general, dada la sofisticación de estos generadores, el análisis de los detalles de implementación de estos algoritmos requiere profundos conocimientos matemáticos.
Si no se elige explícitamente una semilla, Python utilizará típicamente la hora del propio ordenador. En concreto, los milisegundos transcurridos desde la medianoche UTC del 1 de enero de 1970 hasta el momento actual en el que se ejecuta el código. Esta marca temporal (epoch) se conoce como UNIX epoch. Para muchas de las aplicaciones de interés científico, es una elección más que suficiente.
Empezar a usar valores aleatorios en Python es muy simple, importando el módulo estándar random.
import random
Distribuciones uniformes#
Cada vez que ejecutamos el fragmento siguiente, obtenemos diferentes valores.
random.random()
0.30144698574779716
Son valores reales en el intervalo semiabierto \([0,1)\). Estadísticamente, la secuencia de estos valores conforma una distribución uniforme, es decir, tienen la misma probabilidad de ser generados.
Los valores son diferentes porque, cada vez que ejecutamos el fragmento, Python elige internamente una semilla diferente, al ser el tiempo transcurrido desde el UNIX epoch diferente. Sin embargo, si elegimos la misma semilla, usando random.seed(semilla), obtenemos siempre la misma secuencia.
Veámoslo generando 5 veces una lista de 5 valores aleatorios utilizando la misma semilla.
import random
for _ in range(5):
lista = []
semilla = 23 # Cambia este valor para comprobar que la lista cambia a su vez
random.seed(semilla) # Comenta esta línea si quieres que la lista cambie cada vez que se ejecute la celda
for _ in range(5):
lista.append(random.random())
print(lista)
[0.9248652516259452, 0.9486057779931771, 0.8924333440485793, 0.08355067683068362, 0.5920272268857353]
[0.9248652516259452, 0.9486057779931771, 0.8924333440485793, 0.08355067683068362, 0.5920272268857353]
[0.9248652516259452, 0.9486057779931771, 0.8924333440485793, 0.08355067683068362, 0.5920272268857353]
[0.9248652516259452, 0.9486057779931771, 0.8924333440485793, 0.08355067683068362, 0.5920272268857353]
[0.9248652516259452, 0.9486057779931771, 0.8924333440485793, 0.08355067683068362, 0.5920272268857353]
Nótese el uso del identificador _. Se suele usar como indicativo de que el índice del bucle no es necesario y, por tanto, lo ignoramos.
Valores reales distribuidos uniformemente dentro de un rango#
Si queremos obtener valores aleatorios de forma uniforme en un intervalo \([inf,sup]\), disponemos del método uniform(inf, sup), que devuelve un real \(x\) en el intervalo \(inf \leq x \leq sup\).
lista = []
inf = -10.5
sup = 20.8
for _ in range(5):
lista.append(random.uniform(inf, sup))
print(lista)
[2.7632938777542915, 6.0917547166936, -6.421517938953859, -4.490488969020139, 3.415152862225307]
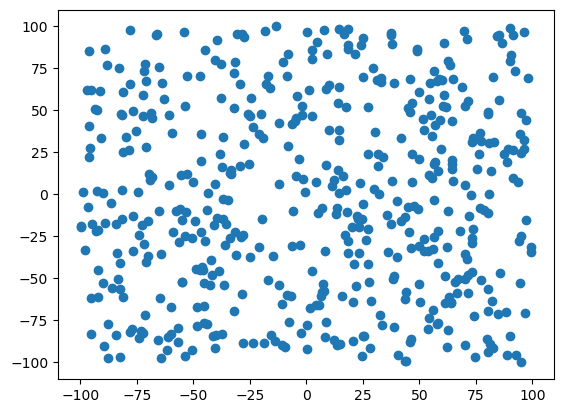
El siguiente ejemplo muestra como generar una nube de puntos aleatorios en 2D. En concreto, \(500\) puntos en el cuadrado formado por los vértices \(\{-100,-100\}\) y \(\{100,100\}\).
import matplotlib.pyplot as plt
inf = -100
sup = 100
num_puntos = 500
x = [0]*num_puntos
y = [0]*num_puntos
for i in range(num_puntos):
x[i] = random.uniform(inf, sup)
y[i] = random.uniform(inf, sup)
plt.scatter(x,y)
<matplotlib.collections.PathCollection at 0x1d89a288890>
Valores enteros distribuidos uniformemente dentro de un rango#
De forma similar, para generar valores enteros uniformemente distribuidos en un rango de valores puede usarse el método randint(inf, sup), que devuelve un entero \(x\) en el intervalo \(inf \leq x \leq sup\).
inf = -10
sup = 6
lista = []
for _ in range(10):
lista.append(random.randint(inf, sup))
print(lista)
[-1, 5, 3, -8, -8, -6, -7, -2, -4, -5]
Distribución normal#
La distribución normal de una variable tiene dos parámetros:
la media \(\mu\)
la desviación típica \(\sigma\)
La función gauss(mu, sigma) devuelve un valor pseudoaleatorio float que sigue esa distribución.
mu = 10
sigma = 1
random.gauss(mu, sigma)
8.747225366700402
Ejemplos de aplicación#
Adivinar un número entero pensado por el ordenador#
Ayudándose del algoritmo de bisección, el usuario deberá calcular a mano (o con ayuda de otro programa en paralelo) la secuencia de valores que permitirá adivinar un número entero generado aleatoriamente por el ordenador.
El programa tendrá las siguientes características:
El usuario fijará un rango inicial de valores enteros.
El programa avisará del número de intentos disponibles.
Mediante un bucle solicitará al usuario la introducción del valor, indicando en el caso de que no se haya acertado si el valor a adivinar es inferior o superior. Si se acierta o se sobrepasa el número máximo de intentos el bucle finalizará.
Mostrar un mensaje indicando si se ha acertado o no y el número de intentos empleado.
Para la introducción del rango de valores se utiliza una función introduce_rango_int(mensaje), que devolverá una tupla con los valores enteros inf y sup del rango. La cadena mensaje permite adaptar el uso de la función a otros cometidos diferentes a los de este ejemplo.
def introduce_rango_int(mensaje=''):
'''
Devuelve una tupla entera (inf, sup), garantizando inf <= sup.
Parameters
----------
mensaje : str
Mensaje por pantalla para indicar el objeto de la solicitud de los valores del rango
Returns
-------
inf, sup : tuple of int
Tupla con los valores enteros del rango
Example
-------
>>> inf, sup = introduce_rango('Introduce un rango de valores:')
'''
print(mensaje)
while True:
try:
inf = int(input('Valor inferior del rango:'))
sup = int(input('Valor superior del rango:'))
if inf > sup:
raise ValueError('No se cumple {} <= {}.'.format(inf, sup))
except ValueError as error:
print(error)
else:
break
return inf, sup
inf, sup = introduce_rango_int()
Para facilitar la introducción de valores por parte del usuario intentando adivinar el número pensado por el ordenador, utilizaremos la función introduce_valor_int(inf, sup).
def introduce_valor_int(inf, sup):
'''
Devuelve un valor entero introducido por teclado por el usuario, tal que inf <= valor <= sup
Parameters
----------
inf, sup : numérico, int
Valores inferior y superior del rango
Returns
-------
valor : int
Entero introducido por teclado por el usuario
Raises
------
ValueError
Si inf > sup
Example
-------
>>> valor = introduce_valor_int(0, 100)
'''
if inf > sup:
raise ValueError('El rango de valores [{},{}] no cumple inf <= sup'.format(inf, sup))
while True:
print('Introduzca un valor entero dentro del rango de valores [{},{}]'.format(inf, sup))
try:
valor = int(input('Valor:'))
if inf > valor or sup < valor:
raise ValueError('El valor introducido no pertenece al rango [{},{}]'.
format(inf, sup))
except ValueError as error:
print(error)
else:
break
return valor
print(introduce_valor_int(0, 100))
Finalmente, el bucle de solicitud de valores al usuario, puede encapsularse en una función adivina_numero(inf, sup).
def adivina_numero(inf, sup):
'''
Devuelve una tupla con el resultado del proceso de adivinación
Parameters
----------
inf, sup : numérico, int
Valores inferior y superior del rango
Returns
-------
exito : bool
True si se ha acertado el número
i+1 : int
Número de intentos empleados
num_intentos_max : int
Número de intentos máximos permitidos, en consonancia con el algoritmo de bisección
valor_a_adivinar : int
Número pensado por el ordenador
Example
-------
>>> exito, num_intentos, num_intentos_max, valor_a_adivinar = adivina_numero(0, 100)
'''
num_intentos_max = int(math.log2(sup-inf+1)+1)
print('Te daré {} oportunidades para acertar.'.format(num_intentos_max))
valor_a_adivinar = random.randint(inf, sup)
exito = False
for i in range(num_intentos_max):
valor = introduce_valor_int(inf, sup)
if valor < valor_a_adivinar:
print('Debes probar con un valor superior.')
elif valor > valor_a_adivinar:
print('Debes probar con un valor inferior.')
else:
exito = True
break
return exito, i+1, num_intentos_max, valor_a_adivinar
El programa principal quedaría como sigue:
# Adivinar un número pensado por el ordenador.
# El usuario elige el rango de valores al que pertenece el número que debe adivinar el programa.
import math
import random
inf, sup = introduce_rango_int('Introduzca el rango de valores enteros al que pertenece el número que debe adivinarse.')
exito, num_intentos, num_intentos_max, valor_a_adivinar = adivina_numero(inf, sup)
if exito:
print('Has acertado en {} intentos.'.format(num_intentos))
else:
print('¡Torpe! Consumiste los {} intentos disponibles.'.format(num_intentos_max))
print('El número que tenías que adivinar es el {}.'.format(valor_a_adivinar))
Un ejemplo de ejecución es el siguiente:
Introduzca el rango de valores enteros al que pertenece el número que debe adivinarse.
Valor inferior del rango:0
Valor superior del rango:100
Te daré 7 oportunidades para acertar.
Introduzca un valor entero dentro del rango de valores [0,100]
Valor:50
Debes probar con un valor inferior.
Introduzca un valor entero dentro del rango de valores [0,100]
Valor:25
Debes probar con un valor inferior.
Introduzca un valor entero dentro del rango de valores [0,100]
Valor:12
Debes probar con un valor superior.
Introduzca un valor entero dentro del rango de valores [0,100]
Valor:18
Debes probar con un valor superior.
Introduzca un valor entero dentro del rango de valores [0,100]
Valor:21
Debes probar con un valor superior.
Introduzca un valor entero dentro del rango de valores [0,100]
Valor:23
Has acertado en 6 intentos.
Cálculo del número \(\pi\)#
Para calcular \(\pi\) vamos a usar un círculo centrado en el origen de radio \(1\), inscrito en un cuadrado de lado \(2\). El área del cuadrado es \(2*2=4\) y el del círculo \(\pi r^2=\pi\).
Por tanto, la relación entre ambas áreas es:
Mediante fuerza bruta podemos generar una secuencia de números aleatorios distribuidos uniformemente dentro del cuadrado. Si relacionamos los que han caído cual dardos dentro del círculo frente a los totales, deberemos obtener un valor que sigue la relación \(\pi/4\).
En lugar de todo el cuadrado, podemos escoger solo el primer cuadrante y utilizar directamente la función random().
def pi_numerico(n):
'''
Devuelve el valor de pi estimado para una muestra de n valores aleatorios usando
el método de los dardos caídos en un círculo inscrito en un cuadrado
Parameters
----------
n : int
Número de ensayos
Returns
-------
pi : float
Valor estimado de pi
Example
-------
>>> pi = pi_numerico(10000)
'''
contador = 0
for _ in range(n):
x = random.random()
y = random.random()
if x*x + y*y < 1:
contador += 1
return 4*contador/n
n = 10000 # Puedes probar con otros valores para ver como varía la precisión
print('La aproximación obtenida para pi con {} dardos es {}'.format(n, pi_numerico(n)))
La aproximación obtenida para pi con 10000 dardos es 3.1344
Podemos simular el algoritmo usando la biblioteca Matplotlib. Para ello, debemos almacenar los valores obtenidos dentro y fuera del círculo en sendas parejas de listas.
import matplotlib.pyplot as plt
n = 10000
contador = 0
x_dentro = []
y_dentro = []
x_fuera = []
y_fuera = []
for _ in range(n):
x = random.random()
y = random.random()
if x*x + y*y < 1.:
contador += 1
x_dentro.append(x)
y_dentro.append(y)
else:
x_fuera.append(x)
y_fuera.append(y)
print('La aproximación obtenida para pi con {} dardos es {}'.format(n, 4*contador/n))
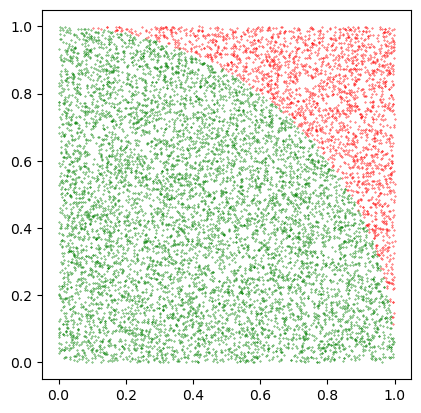
plt.scatter(x_fuera, y_fuera, color='red', s=0.1)
plt.scatter(x_dentro, y_dentro, color='green', s=0.1)
plt.axis('scaled')
plt.show()
La aproximación obtenida para pi con 10000 dardos es 3.1304
Veremos más adelante cómo generar en una sola sentencia una lista de aleatorios cuando estudiemos la biblioteca Numpy.
Creación sintética de un segmento de recta afectado de ruido gaussiano#
Para validar algoritmos en fase de desarrollo es habitual simular determinadas configuraciones de los datos de entrada con valores aleatorios.
En este caso, vamos a crear un segmento de recta sintético al que le vamos a añadir un ruido, una pequeña perturbación a las coordenadas de cada punto. Normalmente se elige un ruido gaussiano, caracterizado por una media \(\mu\) (típicamente 0) y una desviación típica \(\sigma\). Los puntos se generan uniformemente entre ambos extremos.
Este tipo de figuras geométricas con ruido añadido son utilizadas para validar algoritmos de estimación de sus parámetros como, por ejemplo, mínimos cuadrados.
# Dibujando manualmente un segmento de recta aleatorio
import matplotlib.pyplot as plt
def genera_coordenadas_segmento_rnd(p_i, p_f, desv, num_puntos):
'''
Devuelve las listas de num_puntos distribuidos uniformemente en un segmento de recta de puntos
extremos p_i y p_f. Estos puntos tienen además un ruido gaussiano aditivo de media 0
y desviación típica desv.
Parameters
----------
p_i : tuple, float
Tupla con el extremo inicial del segmento
p_f : tuple, float
Tupla con el extremo final del segmento
desv : float
Desviación típica del ruido gaussiano aditivo de media 0
num_puntos : int
Número de puntos aleatorios que se generarán
Returns
-------
lista_x, lista_y : tuple of float
Tupla con las listas de coordenadas de los puntos generados
Example
-------
>>> lista_x, lista_y = genera_coordenadas_segmento_rnd((0, 0), (100, 50), 1.2, 400)
'''
x_i, y_i = p_i
x_f, y_f = p_f
v_x, v_y = (x_f-x_i, y_f-y_i) # (v_x, v_y) Vector director
# Creamos las listas de coordenadas
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i in range(num_puntos):
l = random.random() # Posición aleatoria uniforme del punto dentro del segmento
ruido_x = random.gauss(0, desv)
ruido_y = random.gauss(0, desv)
lista_x[i] = x_i + l*v_x + ruido_x
lista_y[i] = y_i + l*v_y + ruido_y
return lista_x, lista_y
p_i = (100, 50)
p_f = (-150, 300)
num_puntos = 100
desv_std = 3
lista_x, lista_y = genera_coordenadas_segmento_rnd(p_i, p_f, desv_std, num_puntos)
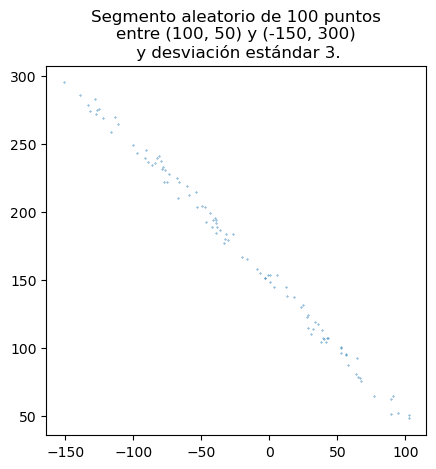
plt.scatter(lista_x, lista_y, s=0.1)
plt.title('Segmento aleatorio de {} puntos\nentre {} y {}\n y desviación estándar {}.'.
format(num_puntos, p_i, p_f, desv_std))
plt.axis('scaled')
plt.show()