Introducción a Matplotlib#
Introducción
Gráficos básicos
Dibujando funciones de una variable
Título y etiquetas en ejes
La función linspace() del paquete Numpy
Ejemplos
Introducción#
El paquete matplotlib es una extensa biblioteca de funciones para generar gráficos 2D y 3D.
Algunas de sus características son:
Curva de aprendizaje suave: ofrece funcionalidades simples para usuarios ocasionales.
Todo tipo de ajustes programables de los elementos de una ventana gráfica.
Gran variedad de formatos de exportación de las figuras.
Matplotlib está construido sobre el paquete Numpy y trabaja de forma natural con los vectores y matrices (arrays) a ella asociados. Veremos más adelante las funcionalidades del paquete Numpy. Pero, por ahora, trabajaremos con las listas nativas de Python (que serán transformadas internamente a numpy arrays en las funciones del paquete Matlotlib). Nótese que restringiremos el uso a listas formadas por valores del mismo tipo de dato.
Aunque no es la forma usual, utilizar en este momento listas nos permite:
visualizar desde ya los resultados de algunos de nuestros ejercicios.
nos obliga a practicar con el manejo de las estructuras de control; no olvidemos que nuestro objetivo es aprender a programar. De la otra forma, muchas operaciones de bajo nivel quedan ocultas detrás de las poderosas herramientas que nos brinda el paquete Numpy.
Dentro del paquete matplotlib destaca el módulo pyplot.
Este módulo oculta muchas de las funcionalidades de bajo nivel de la biblioteca, permitiendo el
uso de sencillas funciones para los elementos gráficos más habituales, tales como creación de figuras, trazado de líneas, visualización de imágenes, inserción de texto, etc.
En la bibliografía podéis encontrar otro módulo llamado pylab que tiene una funcionalidad similar, en apariencia incluso más simple. Sin embargo, su uso está hoy en día desaconsejado por diferentes razones que sería prolijo comentar.
El módulo pyplot emula el entorno de programación gráfica de MATLAB, herramienta software de pago muy popular en universidades y empresas. En la misma línea, ya hemos comentado que Spyder es un IDE muy similar al de MATLAB. Más adelante, en otras asignaturas o en vuestra vida profesional, si necesitáis dar el cambio, éste será sencillo.
Para comenzar usando el módulo pyplot de Matplotlib en un programa Python la forma estándar es:
import matplotlib.pyplot as plt
Gráficos básicos#
Función plot()#
Mediante la función .plot() suministramos una lista para su trazado.
lista = [6, 2, 5, 6, 8, 1, 3, 6, 7, 3]
plt.plot(lista)
[<matplotlib.lines.Line2D at 0x18b8cbe0590>]
Por defecto, .plot(lista) une con una línea la secuencia de puntos de coordenadas \((i,lista[i])\), siendo \(i\) los índices válidos de la lista desde \(0\). En nuestro ejemplo, los puntos \(\{(0,6),(1,2),(2,5),...,(7,6),(8,7),(9,3)\}\).
Debe notarse que la figura donde reside la línea trazada se crea de forma automática para contener el dibujo. No solo eso, en ausencia de indicaciones, se usan diferentes opciones por defecto, como tamaño de la figura, color y grosor de la línea, etc.
Si proporcionamos dos listas, .plot(lista_x, lista_y), se une con una línea la secuencia de puntos de coordenadas \((lista\_x[i],lista\_y[i])\), siendo \(i\) los índices válidos de las listas desde \(0\). Es decir, la primera lista corresponde a las abscisas y la segunda a las ordenadas. Obviamente, ambas listas tendrán el mismo número de elementos. ¿Qué ocurre en caso contrario? ¡Prueba a eliminar un elemento de una de las listas!
plt.plot([1.1, -3.23, 5.3, 7.34, 6.6, 0.1, 2.123, 4.17],
[6, 2, 5.12, 6.25, 8.2, 1, -3.35, 6.3])
[<matplotlib.lines.Line2D at 0x18b8d48e010>]
Función show()#
En los dos ejemplos anteriores el kernel de IPython ha mostrado las figuras sin necesidad del consurso de ninguna función añadida. En realidad, tras la ejecución de una celda, se ha invocado internamente a la función .show(), que es la que de forma efectiva muestra la figura.
Utilizaremos la llamada a la función .show() para ser nosotros quienes controlemos el momento en que se muestra la figura.
plt.plot([1.1, -3.23, 5.3, 7.34, 6.6, 0.1, 2.123, 4.17],
[6, 2, 5.12, 6.25, 8.2, 1, -3.35, 6.3])
plt.show()

Colores y formatos de línea#
Además de los parámetros correspondientes a las listas, la función .plot() admite una cadena con una serie de caracteres dotados de significado como tercer argumento opcional. El significado de los caracteres está prestado de MATLAB: sirven para indicar el color, el tipo de línea y si el punto tiene una marca asociada. El formato por defecto es 'b-', una línea sólida azul (blue). Basta utilizar 'r^--' para que la línea sea roja (r) discontinua (--) con marcas triangulares (^) en los puntos o 'go' para dibujar los puntos circulares (o) de forma aislada en color verde (g).
plt.plot(range(10), 'r^--')
plt.show()
plt.plot(range(10), 'go')
plt.show()
Función scatter()#
Mediante la función .scatter() podemos dibujar los puntos \((lista\_x[i],lista\_y[i])\) sin unir por líneas, apareciendo los puntos de forma dispersa.
Sin ningún tipo de argumento opcional es equivalente a usar la función .plot() con el argumento 'o'.
plt.scatter([1.1, -3.23, 5.3, 7.34, 6.6, 0.1, 2.123, 4.17],
[6, 2, 5.12, 6.25, 8.2, 1, -3.35, 6.3])
plt.show()
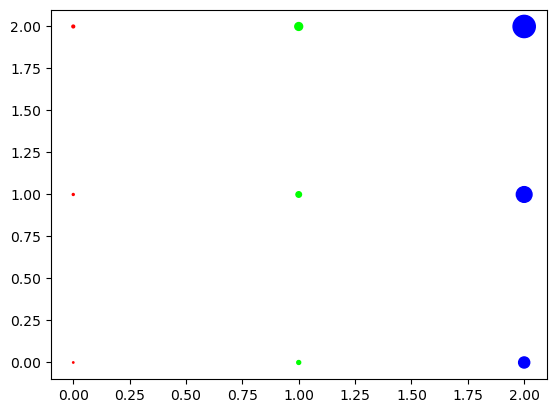
Sin embargo, las posibilidades que ofrece a mayores respecto a .plot() son muy diversas. Por ejemplo, con el parámetro opcional s podemos incluir una lista con los radios deseados de los puntos y con el parámetro opcional c, sus colores. Eso entre otras muchas opciones.
lista_x = []
lista_y = []
radio = 1
radios = []
rojo_verde_azul = [(1, 0, 0), (0, 1, 0), (0, 0, 1)] # Colores R, G y B
colores = []
for i in range(3):
color = rojo_verde_azul[i]
for j in range(3):
lista_x.append(i)
lista_y.append(j)
radios.append(radio)
colores.append(color)
radio *= 2
plt.scatter(lista_x, lista_y, s=radios, c=colores)
plt.show()
Dibujando funciones de una variable#
Un uso habitual de las herramientas gráficas es dibujar una función \(y=f(x)\) para una colección de puntos en un intervalo de valores.
Por ejemplo, supongamos que deseamos dibujar la función \(y=cos^2(x)\) utilizando \(100\) puntos equidistantes en el intervalo \(-2\pi\leq x\leq2\pi\).
import matplotlib.pyplot as plt
import math
num_puntos = 100
x_min = -2*math.pi
x_max = -x_min
# Hay (num_puntos - 1) intervalos incluyendo x_min y x_max
incremento = (x_max - x_min)/(num_puntos - 1)
lista_x = [0]*num_puntos # Rellenamos de 0's ambas listas. Así evitamos usar el método append().
lista_y = [0]*num_puntos
for i in range(num_puntos):
x = x_min + i*incremento # x va tomando los num_puntos equidistantes entre x_min y x_max
lista_x[i] = x
lista_y[i] = math.cos(x)**2
plt.plot(lista_x, lista_y)
plt.show()
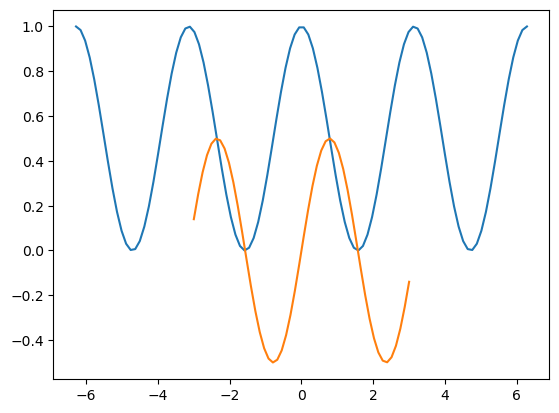
Dibujando varias gráficas superpuestas#
Es muy sencillo dibujar varias funciones superpuestas sin más que invocar a la función .plot() de manera consecutiva, incluso con listas de tamaños diferentes. En el ejemplo, se añade una gráfica de la función \(y=sin(x)cos(x)\) utilizando \(50\) puntos en el intervalo \(-3\leq x\leq3\).
Nótese cómo Matplotlib configura el gráfico de forma automática para adaptarse a los distintos rangos y eligiendo colores diferentes.
num_puntos = 50
x_min = -3
x_max = -x_min
incremento = (x_max-x_min)/(num_puntos - 1)
lista_x2 = [0]*num_puntos
lista_y2 = [0]*num_puntos
for i in range(num_puntos):
x = x_min + i*incremento
lista_x2[i] = x
lista_y2[i] = math.sin(x)*math.cos(x)
plt.plot(lista_x, lista_y)
plt.plot(lista_x2, lista_y2)
plt.show()
Valores indefinidos en la lista de ordenadas#
Aviso
Este apartado requiere haber estudiado el tema Manejo de excepciones.
La función seno cardinal desnormalizada \(sinc(x)\) tiene por ecuación:
En la abscisa \(x=0\), esta función presenta una singularidad evitable, que sabemos por la teoría de límites del cálculo que tiene el valor 1.
Sin embargo, cuando en un programa generamos los posibles valores de una función, no siempre el código está sintonizado para detectar estas singularidades.
Vamos a elegir \(301\) puntos en el intervalo \(-15\leq x\leq15\). Sabemos que vamos a tener problemas si intentamos generar la lista de ordenadas si una de las abscisas es \(0\) .
import math
num_puntos = 301
x_min = -15
x_max = -x_min
incremento = (x_max-x_min)/(num_puntos - 1)
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i in range(num_puntos):
x = x_min + i*incremento
lista_x[i] = x
lista_y[i] = math.sin(x)/x
---------------------------------------------------------------------------
ZeroDivisionError Traceback (most recent call last)
Cell In[11], line 13
11 x = x_min + i*incremento
12 lista_x[i] = x
---> 13 lista_y[i] = math.sin(x)/x
ZeroDivisionError: float division by zero
Vemos que se ha generado la excepción ZeroDivisionError: float division by zero.
Una opción que podemos emplear en este caso particular es evitar añadir a la lista de abscisas el valor \(x=0\). Este método es engorroso, pues, en el caso general, para cada función debemos identificar previamente los valores conflictivos.
Una opción más inteligente es capturar la excepción y, en esos casos, a esos valores conflictivos les asignamos como valor de la función un valor float especial llamado nan, not a number. La buena noticia es que cuando la función .plot() detecta un valor nan en una lista, omite la representación de ese punto.
Por supuesto, de nuestro conocimiento de la teoría de límites, en este ejemplo concreto también podemos asignar el valor \(1\) cuando \(x=0\).
import matplotlib.pyplot as plt
import math
num_puntos = 301
x_min = -15
x_max = -x_min
incremento = (x_max-x_min)/(num_puntos - 1)
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i in range(num_puntos):
x = x_min + i*incremento
lista_x[i] = x
try:
lista_y[i] = math.sin(x)/x
except ZeroDivisionError:
lista_y[i] = float('nan') # Podríamos haber puesto en este ejemplo lista_y[i] = 1
plt.plot(lista_x, lista_y)
plt.show()
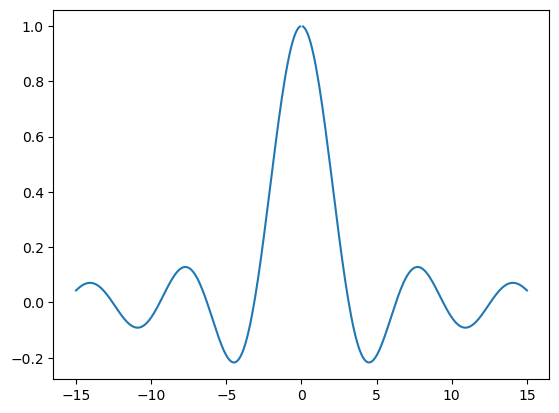
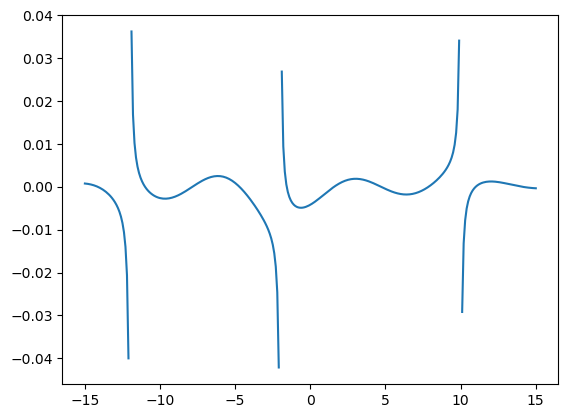
En el siguiente ejemplo, dibujamos la función:
que tiene 3 singularidades, pero nos despreocupamos con el método propuesto de su posición.
# Utilizamos lista de abscisas de la celda anterior
lista_y = [0]*len(lista_x)
for i, x in enumerate(lista_x):
try:
lista_y[i] = math.cos(x)/((x-10)*(x+2)*(x+12))
except ZeroDivisionError:
lista_y[i] = float('nan') # También math.nan si importamos la biblioteca math
plt.plot(lista_x, lista_y)
plt.show()
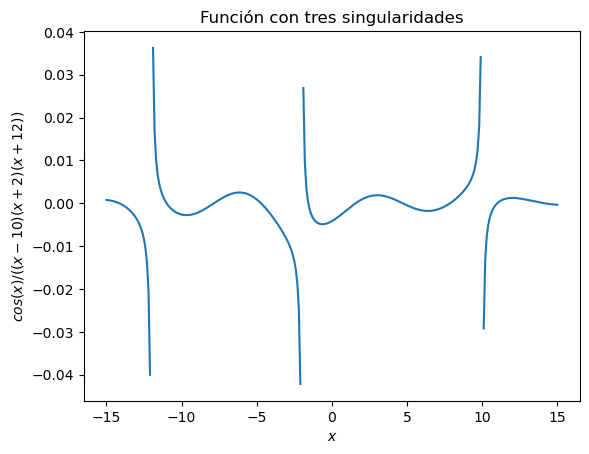
Título y etiquetas en ejes#
Mediante la función .title() podemos añadir un título al gráfico. Mediante las funciones .xlabel() e .ylabel() añadimos etiquetas a los ejes de coordenadas.
plt.plot(lista_x, lista_y)
plt.title('Función con tres singularidades')
plt.xlabel('$x$')
plt.ylabel('${cos(x)}/{((x-10)(x+2)(x+12))}$')
plt.show()
Estas son solo un pequeño ejemplo de las enormes opciones de personalización que ofrece Matplotlib. Iremos viendo algunas más en los ejercicios de laboratorio.
La función linspace() del paquete Numpy#
A lo largo de los ejemplos anteriores, hemos utilizado un método que resulta ciertamente engorroso para generar las abscisas:
Elegimos un límite inferior.
Elegimos un límite superior.
Decidimos cuantos puntos necesitamos.
Calculamos el tamaño del intervalo entre dos abscisas adyacentes.
Generamos la lista correspondiente para usar sus valores como abscisas.
La función .linspace(inf, sup, num_puntos) del paquete Numpy hace todo esto de forma cómoda, proporcionándonos un nivel de abstracción superior y encapsulando todo ese código en una función. Basta introducir los 3 primeros parámetros como argumentos. Para utilizarla, debemos importar el paquete numpy.
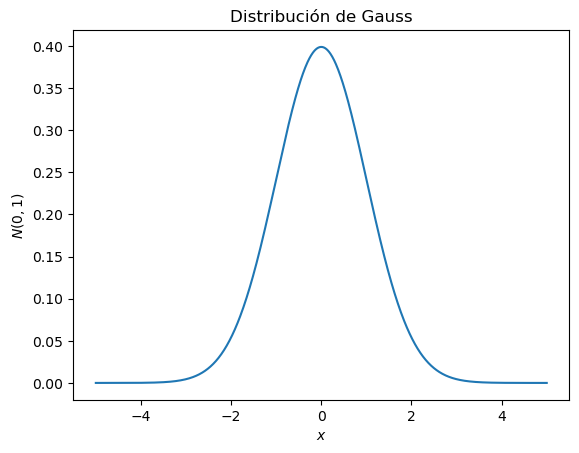
Veámosla en acción para dibujar la función campana de Gauss:
Elegiremos \(1000\) valores en el intervalo \(-5\leq x\leq5\) para una distribución normal de media \(\mu=0\) y desviación estándar \(\sigma=1\).
import matplotlib.pyplot as plt
import numpy as np
import math
num_puntos = 1000
x_min = -5
x_max = 5
lista_x = np.linspace(x_min, x_max, num_puntos)
media = 0
desviacion_estandar = 1
factor = 1./(desviacion_estandar*math.sqrt(2*math.pi))
den = 2*desviacion_estandar**2
lista_y = [0]*num_puntos
for i, x in enumerate(lista_x):
lista_y[i] = factor*math.exp((-(x-media)**2)/den)
plt.plot(lista_x, lista_y)
plt.title('Distribución de Gauss')
plt.xlabel('$x$')
plt.ylabel('$N({},{})$'.format(media, desviacion_estandar))
plt.show()
Ejemplos#
Vamos a ver a continuación cómo dibujar de forma manual dos de los tipos de figuras geométricas bidimensionales más usuales:
un segmento de recta
una circunferencia
Matplotlib ofrece para estas y otras figuras funciones poderosas para hacerlo. Además, algunas operaciones con funciones de biblioteca se hacen de forma más efectiva y compacta con el módulo numpy. Pero recordad que lo que perseguimos es aprender a programar.
Como veremos más adelante, saber crear manualmente puntos pertenecientes a una figura puede sernos de gran utilidad.
Dibujando un segmento de recta#
La ecuación de un segmento de recta#
Un segmento de recta viene definido por sus dos puntos extremos \(\mathbf{p_1}=(x_1,y_1)\) y \(\mathbf{p_2}=(x_2,y_2)\).
Una característica importante es el vector director \(\vec{\mathbf{v}}=(v_x,v_y)\) del segmento, que podemos obtenerlo fácilmente como:
Nótese que cualquier punto del segmento cumple la ecuación:
Esto nos da una idea de cómo pintar \(n\) puntos equidistantes pertenecientes al segmento, incluidos sus extremos. Basta elegir \(n\) valores de \(\lambda\) equidistantes en el intervalo \([0,1]\).
Como acabamos de ver, nos aprovecharemos de la función .linspace() del módulo numpy para generar los valores en el intervalo \([0,1]\).
# Dibujando manualmente un segmento de recta
import matplotlib.pyplot as plt
import numpy as np
num_puntos = 100
lambdas = np.linspace(0, 1, num_puntos) # num_puntos valores equidistantes en el intervalo [0,1]
x1, y1 = 100, 50 # Utilizamos tuplas, aunque podría usarse otro contenedor
x2, y2 = -150, 300
v_x, v_y = (x2-x1, y2-y1) # (vx, vy) Vector director
# Creamos las listas de coordenadas
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i, l in enumerate(lambdas):
lista_x[i] = x1 + l*v_x
lista_y[i] = y1 + l*v_y
plt.scatter(lista_x, lista_y, s=0.1) # s es un parámetro que controla el tamaño del punto
plt.title(f'Segmento de recta entre los puntos {(x1,y1)} y {(x2,y2)}')
plt.axis('scaled') # Esta sentencia hace que la escala de ambos ejes sea la misma
plt.show()
Si el alumno ya ha estudiado a estas alturas funciones, podemos encapsular la mayor parte del código de la celda anterior usando una función genera_coordenadas_segmento().
# Dibujando manualmente un segmento de recta
import matplotlib.pyplot as plt
import numpy as np
def genera_coordenadas_segmento(p1, p2, num_puntos):
'''
Devuelve las listas de num_puntos equidistantes en un segmento de recta de puntos
extremos p_i y p_f.
Parameters
----------
p_i : tuple, float
Tupla con el extremo inicial del segmento
p_f : tuple, float
Tupla con el extremo final del segmento
num_puntos : int
Número de puntos equidistantes que se generarán
Returns
-------
lista_x, lista_y : tuple of float
Tupla con las listas de coordenadas de los puntos generados
Example
-------
>>> lista_x, lista_y = genera_coordenadas_segmento((0, 0), (100, 50), 400)
'''
lambdas = np.linspace(0, 1, num_puntos) # num_puntos valores equidistantes en el intervalo [0,1]
v_x, v_y = (p2[0]-p1[0], p2[1]-p1[1]) # (vx, vy) Vector director
# Creamos las listas de coordenadas
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i, l in enumerate(lambdas):
lista_x[i] = p1[0] + l*v_x
lista_y[i] = p1[1] + l*v_y
return lista_x, lista_y
num_puntos = 100
p1 = (100, 50)
p2 = (-150, 300)
lista_x, lista_y = genera_coordenadas_segmento(p1, p2, num_puntos)
plt.scatter(lista_x, lista_y, s=0.1)
plt.title(f'Segmento de recta entre los puntos {p1} y {p2}')
plt.axis('scaled')
plt.show()

No es muy difícil darse cuenta que si lo único que queremos es dibujar el segmento, hubiese sido mucho más rápido lo siguiente:
# Dibujando manualmente un segmento de recta
import matplotlib.pyplot as plt
p1 = (100, 50)
p2 = (-150, 300)
plt.plot((p1[0], p2[0]), (p1[1], p2[1]))
plt.title(f'Segmento de recta entre los puntos {p1} y {p2}')
plt.axis('scaled')
plt.show()
Dibujando una circunferencia#
La ecuación de una circunferencia#
Una circunferencia viene definida por su centro \(\mathbf{c}=(c_x,c_y)\) y por su radio \(R\).
La forma paramétrica de la ecuación de una circunferencia es la que nos interesa para nuestro problema:
Para pintar \(n\) puntos equidistantes pertenecientes a la circunferencia, basta elegir \(n\) valores de \(\theta\) equidistantes en el intervalo \([0,2\pi]\).
Algún alumno se habrá dado cuenta que para los valores \(0\) y \(2\pi\) de \(\theta\) obtenemos el mismo punto. Aunque podría evitarse, no tiene mayor importancia que esto ocurra.
# Dibujando manualmente una circunferencia
# Aprovechamos que el módulo numpy nos brinda pi, cos() y sin()
import matplotlib.pyplot as plt
import numpy as np
num_puntos = 100
titas = np.linspace(0, 2*np.pi, num_puntos) # num_puntos valores en el intervalo [0,2*pi]
centro = (350, 250)
radio = 75.3
# Creamos las listas de coordenadas
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i, tita in enumerate(titas): # Generamos los num_puntos de la circunferencia
lista_x[i] = centro[0] + radio*np.cos(tita)
lista_y[i] = centro[1] + radio*np.sin(tita)
plt.scatter(lista_x, lista_y, s=0.1)
plt.title(f'Circunferencia de centro {centro} y radio {radio}')
plt.axis('scaled')
plt.show()
Si el alumno ya ha estudiado a estas alturas funciones, podemos de nuevo encapsular código usando una función genera_coordenadas_circunferencia().
# Dibujando manualmente una circunferencia
# Aprovechamos que el módulo numpy nos brinda pi, cos() y sin()
import matplotlib.pyplot as plt
import numpy as np
def genera_coordenadas_circunferencia(centro, radio, num_puntos):
'''
Devuelve las listas de num_puntos equidistantes en una circunferencia
de parámetros radio y centro.
Parameters
----------
centro : tuple, float
Tupla con las coordenadas del centro
radio : float
Valor del radio
num_puntos : int
Número de puntos equidistantes que se generarán
Returns
-------
lista_x, lista_y : tuple of float
Tupla con las listas de coordenadas de los puntos generados
Example
-------
>>> lista_x, lista_y = genera_coordenadas_circunferencia((100, 50), 23.5, 500)
'''
titas = np.linspace(0, 2*np.pi, num_puntos) # num_puntos equidistantes en el intervalo [0,2*pi]
# Creamos las listas de coordenadas
lista_x = [0]*num_puntos
lista_y = [0]*num_puntos
for i, tita in enumerate(titas): # Generamos los num_puntos de la circunferencia
lista_x[i] = centro[0] + radio*np.cos(tita)
lista_y[i] = centro[1] + radio*np.sin(tita)
return lista_x, lista_y
num_puntos = 100
centro = (350, 250)
radio = 75.3
lista_x, lista_y = genera_coordenadas_circunferencia(centro, radio, num_puntos)
plt.scatter(lista_x, lista_y, s=0.1)
plt.title(f'Circunferencia de centro {centro} y radio {radio}')
plt.axis('scaled')
plt.show()

Matplotlib tiene una función llamada Circle() que permite dibujar círculos, pero se requiere de una serie de etapas previas de configuración de la figura que ahora mismo no merece la pena explicar.
Cuando estudiemos Numpy veremos como, en muchas ocasiones, la creación de listas de ordenadas a partir de listas de abscisas se puede hacer de forma mucho más compacta usando las herramientas de esa biblioteca.
