Ejemplos¶

En los siguientes ejemplos vamos a utilizar todas las herramientas de programación vistas hasta el momento:

Entrada y salida de datos
Control de flujo condicional
Control de flujo iterativo

Simulación de la multiplicación entera hardware¶

Descripción del algoritmo¶

El producto \(P\) de dos enteros positivos \(x\) e \(y\), \(P=x*y\), podemos calcularlo de forma iterada introduciendo un término \(P_i\) en la expresión, de tal forma que, en la iteración \(i=0\):

\[\begin{split} & P_{0}=0 \\ P=P_0+x_{0}*y_{0}\quad \mbox{con} \quad & x_{0}=x \\ & y_{0}=y\end{split}\]

La iteración \(i+1\) se obtiene de la anterior \(i\) de la siguiente forma:

Si \(y_i\) es un número par (en binario su digito más a la derecha es un 0)

\[\begin{split}y_{i+1} &= y_i/2 \quad \,\,\, \rightarrow \quad \mbox{Desplazamiento de un bit en hardware hacia la} \textbf{ derecha} \\ x_{i+1} &= x_i*2 \quad \rightarrow \quad \mbox{Desplazamiento de un bit en hardware hacia la} \textbf{ izquierda}\\ P_{i+1} &= P_i\end{split}\]

Es fácil verificar que el valor inicial de \(P\) no varía:

\[P = P_i+x_i*y_i=P_i+(x_i*2)*(y_i/2)=P_{i+1}+x_{i+1}*y_{i+1}\]
Si \(y_i\) es un número impar (en binario su digito más a la derecha es un 1)

\[\begin{split}y_{i+1} &= y_i-1 \quad \rightarrow \quad \mbox{Cambiar el bit más a la derecha a 0} \\ x_{i+1} &= x_i \\ P_{i+1} &= P_i + x_i\end{split}\]

De nuevo, el valor de \(P\) no varía:

\[P = P_i+x_{i}*y_{i}=P_i+x_i+x_i*(y_i-1)=P_{i+1}+x_{i+1}*y_{i+1}\]

El proceso iterativo finalizará en la iteración \(n\) en la que \(y_n=0\), y entonces \(P=P_n\).

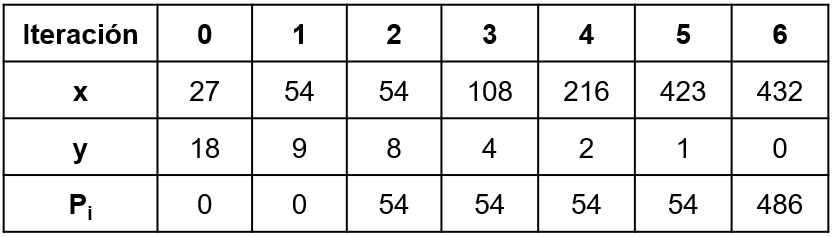
Multiplicación simulando el hardware de 27*18¶

Diseño del programa¶

Datos de entrada

Se solicitará al usuario que introduzca dos valores enteros x e y.

Datos de salida

Se mostrará por pantalla el producto x*y con un mensaje del tipo (x)*(y)=p.

Procesamiento de los datos

Utilizaremos una variable producto para almacenar el resultado. Esta variable irá tomando los diferentes valores \(P_i\) descritos en el algoritmo.

Si alguno de los datos de entrada x o y es 0, el programa terminará inmediatamente con producto=0;

Hay que tener en cuenta que el usuario introducirá valores enteros, tanto positivos como negativos. Dado que el algoritmo está diseñado para números enteros positivos deberemos tener en cuenta el signo del resultado. Para ello, usaremos una variable auxiliar signo tal que:

Si el signo de x e y coincide, entonces signo=1;
Si el signo de x e y difiere, signo=-1;

De esta forma, trabajaremos con el valor absoluto de x e y y, al final, corregiremos con el signo correcto.

Para realizar las iteraciones usaremos un bucle while, puesto que no sabemos cuántas iteraciones serán necesarias.

La salida del bucle se producirá cuando la expresión y sea falsa, es decir, cuando se cumpla y==0.

¿Cómo programamos expresiones tales como \(x_{i+1}=x_i*2\) ?

Simplemente con x=x*2;. El valor de x, \((x_i)\), a la derecha de = se pierde (iteración \(i\)) para obtener un nuevo valor x, \((x_{i+1})\), a la izquierda de =, (iteración \(i+1\)).

Dentro del while solo queda establecer los nuevos valores de x, y y producto en función de si y es par o impar.

Una posible implementación del algoritmo es la siguiente. Nótese la habitual secuencia entrada de datos, algoritmo y salida de resultados.

#include <iostream>
using namespace std;

int main()
{
   // ENTRADA DE DATOS ///////////////////////
   int x, y;
   cout << "Introduzca valor x:";
   cin >> x;
   cout << "Introduzca valor y:";
   cin >> y;

   // ALGORITMO /////////////////////////////
   int producto = 0;
   int signo = 1;

   // El siguiente cout se coloca aqui dado que las variables
   // x e y van a cambiar su valor a lo largo de las iteraciones
   cout << "(" << x << ")*(" << y << ")=";

   if (x != 0 && y != 0) // Si alguno es 0 no hacemos nada, producto=0.
   {
      if ( (x > 0 && y < 0) || (x < 0 && y > 0) )
         signo = -1;

      // Una vez calculado el signo trabajamos con x e y positivas
      if (x < 0)
         x *= -1;
      if (y < 0)
         y *= -1;

      while (y)
      {
         if (y % 2)  // Es impar
         {
            producto += x;
            y = y - 1;
         }
         else
         {
            x = x*2;
            y = y/2;
         }
      }
   }

   // SALIDA DE RESULTADOS //////////////////
   cout << signo*producto << endl;
}

Edita, compila y ejecuta el código

Sucesiones homogéneas recurrentes de orden 2¶

Descripción del algoritmo¶

Una sucesión recurrente homogénea de orden \(t\) es aquella cuyos términos \(x_i\) vienen dados por la expresión:

\[x_{n+t}=c_1x_{n+t-1}+c_2x_{n+t-2}+ ... + c_{t-1}x_{n+1}+c_tx_n\]

donde los coeficientes \(c_i\) de la sucesión son fijos.

Nótese que para poder generar la sucesión necesitamos los \(t\) primeros términos.

Dado que aún no hemos estudiado vectores, que nos permitirían atacar el problema de forma general, vamos a centrarnos en las sucesiones homogéneas recurrentes de orden 2:

\[x_{n+2}=c_1x_{n+1}+c_2x_n\]

Un ejemplo de sucesión recurrente homogénea de orden 2 es la sucesión de Fibonacci, que viene definida por:

\[\begin{split}\mbox{Coeficientes} \quad & c_1=c_2=1\\ \mbox{Valores iniciales} \quad & x_0=0 \, ,x_1=1\end{split}\]

La sucesión fue dada a conocer en occidente por Leonardo de Pisa (alias Fibonacci) como la solución a un problema de la cría de conejos con los siguientes supuestos:

A partir de una pareja de conejos en una granja, cuantas parejas se obtendrían al cabo de un año sabiendo que:

Una pareja desde que nace tarda dos meses en reproducirse

A partir del 2º mes, se reproduce cada mes

Cada camada es otra pareja

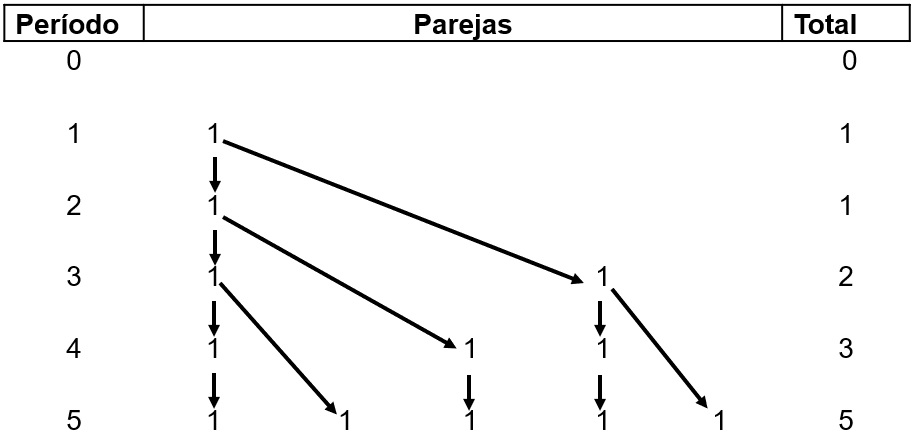
Sucesión de Fibonacci¶

La evolución de las parejas de conejos es la siguiente:

Al inicio del primer periodo se introduce una pareja.
Al inicio del segundo periodo solamente tenemos una pareja.
Al inicio del tercer periodo (han pasado dos meses) tenemos la pareja inicial más sus crías, en total, 2 parejas.
Al inicio del cuarto periodo se ha vuelto a reproducir la pareja inicial, por lo que tenemos 3 parejas, y así sucesivamente.

La sucesión de Fibonacci vendría dada entonces por los valores \(0,1,1,2,3,5,8,13,21,34,…\)

Diseño del programa¶

El programa mostrará por pantalla los \(n\) primeros términos de la sucesión y, como resultado final, mostrará su suma y la ratio entre el último y el penúltimo término.

Supondremos coeficientes y términos enteros.

Datos de entrada

Solicitará al usuario:

el valor num_terminos, exigiendo con utilizando un bucle do while que sea mayor que 2.
los coeficientes fijos c1 (\(c_1\)) y c2 (\(c_2\))
los dos primeros términos de la sucesión t0 (\(x_0\)) y t1 (\(x_1\))

Datos de salida

Dado que con los conocimientos actuales no sabemos almacenar en un vector los términos obtenidos, el programa irá mostrando por pantalla los valores de la sucesión según se vayan calculando. Al finalizar, se mostrarán:

la suma de los términos
la ratio entre el último y el penúltimo término. En el caso de la sucesión de Fibonacci, este valor converge en el número áureo.

Procesamiento de los datos

Inicializaremos el sumatorio, suma, de los términos a suma = t1 + t0;.

Dado que sabemos cuántos términos hay que calcular, el bucle iterativo adecuado es for.

Como disponemos de los 2 primeros valores, el bucle se inicializará con el contador i igual a 2 y finalizará cuando i < num_terminos sea falso.

¿Cómo programamos expresiones recurrentes tales como \(x_{n+2}=c_1x_{n+1}+c_2x_n\) ?

Vamos a utilizar una variable nuevo_termino para \(x_{n+2}\). Una vez obtenido nuevo_termino = c1*t1 + c2*t0; basta actualizar para la siguiente iteración los nuevos valores de t0 y t1:

for (int i = 2; i < num_terminos; ++i)
{
   int nuevo_termino = c1*t1 + c2*t0;
   cout << " " << nuevo_termino;
   t0 = t1;
   t1 = nuevo_termino;
   suma += nuevo_termino;
}

Dentro del bucle también:

mostramos por pantalla el valor del término recién calculado
actualizaremos el valor del sumatorio de términos suma

Fuera del bucle calcularemos la ratio, ratio = t1/t0;

A continuación mostramos una posible implementación del programa.

// Sucesion recurrente homogenea de orden 2
#include <iostream>
using namespace std;
int main()
{
   int num_terminos;
   do
   {
      cout << "Introduzca el número de términos:";
      cin >> num_terminos;
      if (num_terminos <= 2)
         cout << " El número de términos debe ser superior a 2.\n";
   }
   while (num_terminos <= 2);

   int c1, c2;
   cout << "Introduzca coeficiente c1 (Xn2=c1*Xn1+c2*Xn):";
   cin >> c1;
   cout << "Introduzca coeficiente c2 (Xn2=c1*Xn1+c2*Xn):";
   cin >> c2;
   int t0, t1;
   cout << "Termino de la sucesion x0 (Xn2=c1*Xn1+c2*Xn):";
   cin >> t0;
   cout << "Termino de la sucesion x1 (Xn2=c1*Xn1+c2*Xn):";
   cin >> t1;

   int suma = t0 + t1;
   cout << "Los términos de la sucesion son " << t0 << " " << t1;
   for (int i = 2; i < num_terminos; ++i)
   {
      int nuevo_termino = c1*t1 + c2*t0;
      cout << " " << nuevo_termino;
      t0 = t1;
      t1 = nuevo_termino;
      suma += nuevo_termino;
   }

   cout.precision(20);
   double ratio = static_cast<double>(t1)/t0;

   cout << "\nLa suma de los términos es " << suma;
   cout << "\nEl ratio es " << ratio << endl;
}

Edita, compila y ejecuta el código

Dejamos al alumno que implemente una variante de este programa. Consiste en calcular los términos de la sucesión hasta que un término supere en valor absoluto un valor, valor_maximo, preestablecido en la entrada de datos.

Cálculo del máximo común divisor de dos números enteros¶

Descripción del algoritmo¶

Se trata de encontrar el mayor número que divida exactamente dos números enteros no negativos dados. El algoritmo que resuelve el problema es uno de los más antiguos y famosos y se atribuye a Euclides.

Sean dos enteros positivos \(p\) y \(q\) tal que \(p \ge q\). En general, se puede plantear lo siguiente:

\[p=q*b+r\]

Al dividir \(p\) entre \(q\) se obtiene un cociente \(b\) y un resto \(r\). Es fácil demostrar que el máximo común divisor de \(p\) y \(q\), \(\mbox{mcd}(p,q)\), es el mismo que el de \(q\) y \(r\), \(\mbox{mcd}(q,r)\).

\[\mbox{mcd}(p,q) = \mbox{mcd}(q,r)\]

Este razonamiento puede repetirse cuantas veces se quiera, haciendo que el dividendo sea el anterior divisor y el nuevo divisor el antiguo resto, hasta que eventualmente, con toda seguridad, se obtendrá un resto igual a cero (puesto que los sucesivos restos van inevitablemente descendiendo y deben ser positivos). Cuando el resto es cero, el último divisor que se utilizó es precisamente el máximo común divisor.

Dos casos especiales:

Si el divisor inicial es \(0\), \(\mbox{mcd}(p,0)=p\)
Si dividendo y divisor son ambos nulos, \(\mbox{mcd}(0,0)=0\).

Diseño del programa¶

Datos de entrada

Solicitará al usuario dos enteros, num1 y num2, exigiendo que no sean negativos.

Datos de salida

Mostrará por pantalla el valor del máximo común divisor, mcd, obtenido.

Procesamiento de los datos

Deberemos identificar cuál de los valores de entrada es el mayor y cuál es el menor, para asignarles el rol de dividendo, dividendo, y divisor, divisor, respectivamente.

En este punto también se analizará si uno o ambos valores son nulos para mostrar el resultado predeterminado correspondiente.

Para ir obteniendo de forma iterada los diferentes valores correspondientes a dividendo y divisor utilizaremos un bucle. Dado que no sabemos el número de iteraciones, el bucle apropiado es while. Un do while no es oportuno en este caso porque si de entrada el resto es nulo, no será necesario iterar.

A continuación mostramos una posible implementación del programa.

#include <iostream>
using namespace std;

int main()
{
   int num1, num2;
   // ENTRADA DE DATOS
   do
   {
      cout << "Introduzca un número >=0: ";
      cin >> num1;
      cout << "Introduzca otro número >=0: ";
      cin >> num2;
   } while (num1 < 0 || num2 < 0);

   // ALGORITMO MCD
   int dividendo = num1, divisor = num2;
   if (num1 < num2) //Asegurando que el dividendo sea mayor que el divisor
   {
      divisor = num1;
      dividendo = num2;
   }

   int mcd = 0;
   if (dividendo > 0)
   {
      if (divisor == 0)
         mcd = dividendo;
      else // Algoritmo de Euclides
      {
         while (int resto = dividendo % divisor)
         {
            dividendo = divisor;
            divisor = resto;
         }
         mcd = divisor;
      }
   }

   // SALIDA
   cout << "mcd(" << num1 << "," << num2 << ")=" << mcd << endl;
}